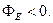Поток и дивергенция векторного поля
Введем понятие элементарного потока вектора
где d Ф Е = Е × dS × cosφ, Е × cosφ = Еn, d Ф Е = Еn × dS. (13.6) Полный поток вектора есть скалярная физическая величина, определяемая формулой
Рис. 13.1. К понятию потока вектора напряженности поля полный поток через замкнутую (гауссову) поверхность S
Аналогично определяется поток магнитного поля. Выясним смысл понятия потока вектора напряженности ФE. Для бесконечно малой плоской площадки dS, помещенной в поле, величина потока Гидродинамическая аналогия: поток вектора скорости несжимаемой жидкости через воображаемую поверхность S пропорционален количеству жидкости, протекающему через эту поверхность в положительном направлении ее нормали за единицу времени. Отсюда и произошло название - "поток". Если поверхность замкнутая, то величина полного потока поля через нее приобретает новый смысл. Сравним картину силовых линий полей, изображенных на рис.13.2. В поле на рис.13.2а силовые линии расходятся из некоторого центра, лежащего внутри S, поэтому почти всюду
Рис.13.2. Примеры различных значений потока вектора
Точка, из которой выходят силовые линии, как из центра, называется источником (истоком) поля. В электрическом поле источниками служат положительные электрические заряды. Места схождения силовых линий называют отрицательными источниками, или стоками. В электрическом поле стоками служат отрицательные электрические заряды. Названия сток и исток опять-таки взяты из гидродинамики. В электромагнитное поле, разумеется, ничего не течет, не истекает и не стекает, но гидродинамическая терминология все же применяется, как весьма наглядная.
|

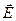 через площадку dS:
через площадку dS: , (13.5)
, (13.5)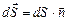 . Тогда
. Тогда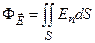 . (13.7)
. (13.7)
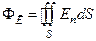 . (13.8)
. (13.8)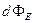 зависит, очевидно, от густоты силовых линий в этом месте поля, от величины площадки и от ее ориентации относительно направления поля. Вспомним, что по условиям построения силовых линий поля их густота должна быть пропорциональна напряженности поля. Следовательно, величина
зависит, очевидно, от густоты силовых линий в этом месте поля, от величины площадки и от ее ориентации относительно направления поля. Вспомним, что по условиям построения силовых линий поля их густота должна быть пропорциональна напряженности поля. Следовательно, величина 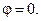 Поэтому для поверхности конечных размеров и произвольной формы величина потока (13.8) отражает не полное число силовых линий, а разницу между числом силовых линий, проходящих в положительном и отрицательном направлениях.
Поэтому для поверхности конечных размеров и произвольной формы величина потока (13.8) отражает не полное число силовых линий, а разницу между числом силовых линий, проходящих в положительном и отрицательном направлениях.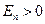 и Ф E > 0, в то время как для поля на рис.13.26,очевидно, Ф E =0 (за положительное направление
и Ф E > 0, в то время как для поля на рис.13.26,очевидно, Ф E =0 (за положительное направление  для замкнутых поверхностей всегда берут направление внешней нормали). Таким образом, Ф Е характеризует то, что можно назвать степенью расходимости силовых линий поля в той области, где находится данная замкнутая поверхность. Расходимость отсутствует, если Ф Е = 0, для сходящихся силовых линий /рис. 13.2в/
для замкнутых поверхностей всегда берут направление внешней нормали). Таким образом, Ф Е характеризует то, что можно назвать степенью расходимости силовых линий поля в той области, где находится данная замкнутая поверхность. Расходимость отсутствует, если Ф Е = 0, для сходящихся силовых линий /рис. 13.2в/