Принцип суперпозиции полей
Вернемся к задаче изучения источников электромагнитного поля. Мы уже знаем, какое поле создает вокруг себя одиночный заряд. Теперь мы хотим найти способы расчёта полей различных систем зарядов. Можно ожидать, что поле системы есть результат сложения полей всех входящих в ее состав элементарных зарядов, но как эти поля складываются? Влияют ли они друг на друга, или каждый из зарядов системы вносит свой вклад в результирующее поле независимо от остальных? Чтобы уяснить смысл этой проблемы, рассмотрим конкретную ситуацию. Пусть в нашем распоряжении имеются три точечных заряда q1, q2 и q3.. Для простоты будем считать их неподвижными. Поместив пробный заряд q в произвольную точку поля, образованного вышеуказанными тремя зарядами. Найдем сначала поочередное, а затем одновременное воздействие на него трех наших зарядов. Оказывается:
Отсюда непосредственно вытекает справедливость следующего выражения:
Опыт показывает, что по такому же принципу складываются поля движущихся зарядов, отдельно - электрические компоненты и отдельно - магнитные. Этот опытный факт, будучи обобщен на системы с любым числом произвольно движущихся зарядов, носит название принципа суперпозиции. Сформулируем его еще раз в полном виде: электромагнитное поле произвольной системы зарядов есть результат сложения полей, которые создавались бы каждым из элементарных зарядов этой системы в отсутствие остальных. При этом компоненты результирующего поля находятся раздельным векторным сложением электрических и магнитных компонент исходных элементарных полей:
Принцип суперпозиции вместе с формулами поля точечного заряда позволяет свести проблему нахождения электромагнитное полей различных систем к чисто математической задаче вычисления сумм (см.выше). Зная величину, расположение и характер движения всех зарядов, входящих в состав системы, мы можем рассчитать ее поле, подставив в вышеприведенные формулы значения
|

 (13.1)
(13.1)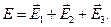 (13.2)
(13.2) (13.3)
(13.3) и
и 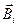 , определяемые для каждого заряда в отдельности. Если распределение зарядов в системе можно считать непрерывным, то суммирование заменяется интегрированием
, определяемые для каждого заряда в отдельности. Если распределение зарядов в системе можно считать непрерывным, то суммирование заменяется интегрированием (13.4)
(13.4)


