Электростатическое поле равномерно заряженной сферы (или проводящего шара)
Учитывая симметрию поля, в качестве гауссовых поверхностей выбираем сферические поверхности, центры которых совпадают с центром сферы (шара) (рис. 14.7).
Рис. 14.7. К расчету поля сферы Разобьем пространство на две области: а) r 1 < R – внутри сферы S . Внутри этой гауссовой поверхности зарядов нет (Q = 0) и, следовательно, Е = 0. б) r 2 > R – вне сферы S. Поскольку Тогда
где
– поверхностная плотность заряда. Модуль вектора напряженности электростатического поля заряженной сферы равен
Электростатическое поле равномерно заряженного непроводящего шара Учитывая симметрию поля, в качестве гауссовых поверхностей выбираем сферические поверхности, центры которых совпадают с центром шара (рис. 14.8).
Рис. 14.8. К расчету поля шара Поскольку Напряженность поля внутри (r 1 < R) и снаружи (r 2 > R) непроводящего шара: а) r 1 < R
где q – заряд в объеме V 1, ограниченном поверхностью S 1,
где
– объемная плотность заряда.
б) r 2 > R (шар находится в вакууме)
где Q – заряд данного шара.
Модуль вектора напряженности поля непроводящего заряженного шара:
|
, то En = E, а при фиксированном r 
Е = const, тогда
,(14.27)
,(14.28)
, (14.29)
= const (14.30)
(14.31)
, то En = E, а при фиксированном r 
, (14.32)
– диэлектрическая проницаемость вещества шара.
. (14.33)
, (14.34)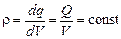
(14.35)
,(14.36)
.(14.37)
(14.38)
