Теорема Гаусса о потоке
вектора Поток вектора напряженности электростатического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную
При непрерывном распределении заряда
где V - объем внутри поверхности S. Уравнение теоремы Гаусса в дифференциальной форме –
где
- расходимость (дивергенция) вектора Дивергенция вектора напряженности поля характеризует локальную степень расходимости силовых линий поля. Если Замечания: I. Теорема Гаусса - это констатация факта существования электрических зарядов, а также того, что силовые линии электрического поля начинаются и кончаются на зарядах. 2. Теорема Гаусса - удобный и простой метод для вычисления электростатических полей. 13.3.2.Поток и дивергенция вектора Поток вектора
В дифференциальной форме это уравнение выражается так:
где Следовательно, магнитостатическое поле – вихревое непотенциальное и не имеет точечных источников. Всюду ли
|
.
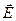(в системе СИ) и диэлектрическую проницаемость среды 
:
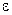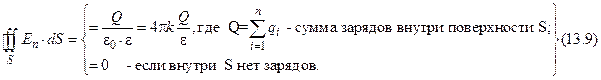
, (13.10)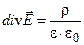
, (13.11)
(13.12)
, r – объёмная плотность заряда.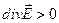
, то поле – расходящееся, в противном случае – поле сходящееся.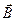
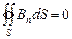;(13.13)
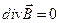, (13.14)
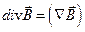– расходимость (дивергенция) вектора 
.
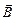