Упорядоченный линейный вывод в ЛППП.
Будем считать, что литеры в клозе упорядочены. Для того чтобы сохранять информацию об отрезанных литерах, они не удаляются, а только обрамляются. Если на каком-то шаге получается клоз, содержащий две одинаковые литеры, то оставляется самая левая из них, после чего отбрасываются все обрамлённые литеры, за которыми не следуют необрамлённые. Эта операция называется отождествлением влево. Если в упорядоченном клозе последняя литера унифицируется с отрицанием одной из обрамлённых литер, то клоз называется редуцируемым и производится его редукция, то есть: 1) удаляется последнюю литеру и обрамленную литеру, с отрицанием которой унифицируется последняя литера; 2) отбросываются все обрамлённые литеры, за которыми не следуют необрамлённые. Например, pÚqÚsÚùq pÚ p //Пример переделать под ЛППП (14)
P (b) Упорядоченной бинарной резольвентой (упорядоченной резольвентой) клозов C1 и C2, содержащих контрарные литеры L1 и L2 (причем L1 – последняя литера в клозе C) называется клоз C вида C={C1¢}È{C2/L2}, где C1¢ получен из С1 путём обрамления последней литеры. Например, pÚq ùqÚr pÚqÚr //пример переделать под ЛППП (15) {b/x} P (x) Ú Q (x, f (a))
Упорядоченным линейным выdодом (OL-выводом) пустого клоза из S (OL-опровержением множества S) называется вывод, удовлетворяющий следующим условиям: 1) отрезаемая литера всегда последняя; 2) вывод имеет следующий вид:
//cхему подправить (12 – аналогично)
где Сi - центральные клозы, Вj - боковые. Боковой клоз всегда выбирается либо из входного множества, либо среди клозов, полученных на предыдущих шагах. Клоз C называется верхним в выводе. OL-вывод является так называемой почти полной стратегией. Теорема о полноте OL-вывода. Если множество клозов S противоречиво, а множество {S/C} - выполнимо, где C Примечание. На практике в роли верхнего клоза выступает отрицание утверждения доказываемой теоремы. Если оно распадается на несколько клозов, то их можно доказывать в отдельности. В этом случае дополнительное условие сводится к естественному требованию множества исходных утверждений.
|


 P (x) Ú Q (x, f (x)) Ú S (y) Ú ù Q (x, f (b))
P (x) Ú Q (x, f (x)) Ú S (y) Ú ù Q (x, f (b))

 {b/x}
{b/x} P (b) Ú Q (b, f(b)) Ú S (y) Ú ù Q (b, f))
P (b) Ú Q (b, f(b)) Ú S (y) Ú ù Q (b, f)) ùQ (b, a) Ú R (z)
ùQ (b, a) Ú R (z) P (b) Ú Q (b, f (a)) Ú R (z)
P (b) Ú Q (b, f (a)) Ú R (z)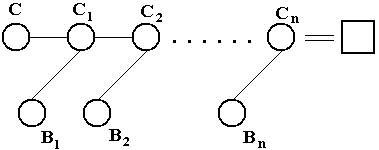
 S, то существует OL-вывод пустого клоза из S с верхним дизъюнктом C.
S, то существует OL-вывод пустого клоза из S с верхним дизъюнктом C.


