Пример 2. Рассмотрим систему двух уравнений с пятью неизвестными (m = 2, n = 5).
Рассмотрим систему двух уравнений с пятью неизвестными (m = 2, n = 5). x1 + x2 + 4x3 + 2x4 + 3x5 = 8, 4x1 + 2x2 + 2x3 + x4 + 6x5 = 4. Определим различные решения этой системы. Количество положительных базисных решений равно I. Допустимое базисное решение. Нулевые (небазисные) переменные: x2, x4, x5. Уравнения: x1 + 4x3 = 8, 4x1 + 2x3 = 4. Решение: единственное решение x1 = 0, x3 = 2. Заключение: базисное решение допустимо, т.к. x1, x3 ≥ 0. II. Недопустимое базисное решение. Нулевые (небазисные) переменные: x3, x4, x5. Уравнения: x1 + x2 = 8, 4x1 + 2x2 = 4. Решение: единственное решение x1 = -6, x2 = 14. Заключение: базисное решение недопустимо, т.к. x1 < 0. III. Решение не единственное. Нулевые (небазисные) переменные: x1, x2, x5. Уравнения: 4x3 + 2x4 = 8, 2x3 + x4 = 4. Решение: единственного решения не существует, т.к. уравнения зависимы. Заключение: бесконечное количество решений. IV. Решения не существует. Нулевые (небазисные) переменные: x1, x3, x4. Уравнения: x2 + 3x5 = 8, 2x2 + 6x5 = 4. Решение: решения не существует, т.к. уравнения несовместны. Заключение: решения не существует. V. Недопустимое базисное решение Нулевые (небазисные) переменные: x2, x3, x5. Уравнения: x1 + 2x4 = 8, 4x1 + x4 = 4. Решение: единственное решение x1 = 14, x4 = -3. Заключение: базисное решение недопустимо, т.к. x4 < 0. VI. Допустимое базисное решение Нулевые (небазисные) переменные: x2, x3, x4. Уравнения: x1 + 3x5 = 8, 4x1 + 6x5 = 4. Решение: единственное решение x1 = 10/3, x5 = 14/9. Заключение: базисное решение допустимо, т.к. x1, x5 ≥ 0. VII. Допустимое базисное решение. Нулевые (небазисные) переменные: x1, x4, x5. Уравнения: x2 + 4x3 = 8, 2x2 + 2x3 = 4. Решение: единственное решение x2 = 0, x3 = 2. Заключение: базисное решение допустимо, т.к. x2, x3 ≥ 0. VIII. Допустимое базисное решение. Нулевые (небазисные) переменные: x1, x3, x5. Уравнения: x2 + 2x4 = 8, 2x2 + x4 = 4. Решение: единственное решение x2 = 0, x4 = 4. Заключение: базисное решение допустимо, т.к. x2, x4 ≥ 0. IX. Допустимое базисное решение. Нулевые (небазисные) переменные: x1, x2, x4. Уравнения: 4x3 + 3x5 = 8, 2x3 + 6x5 = 4. Решение: единственное решение x3 = 2, x5 = 0. Заключение: базисное решение допустимо, т.к. x3, x5 ≥ 0. X. Допустимое базисное решение. Нулевые (небазисные) переменные: x1, x2, x3. Уравнения: 2x4 + 3x5 = 8, x4 + 6x5 = 4. Решение: единственное решение x4 = 4, x5 = 0. Заключение: базисное решение допустимо, т.к. x4, x5 ≥ 0.
На следующем шаге рассмотрим свободные переменные и базисные решения. Напомним, что в стандартной форме записи задачи ЛП свободная переменная xj должна быть представлена как разность двух неотрицательных переменных xj = xj+ - xj-, где xj+, xj- ≥ 0. Основываясь на определении базисного решения, следует, что xj+ и xj- не могут одновременно быть базисными переменными, т.к. они являются взаимозависимыми. Зависимость следует из того, что в ограничении коэффициент при xj+ имеет знак, противоположный знаку коэффициента при xj-. Это означает, что в любом базисном решении, по крайней мере, одна из переменных xj+ и xj- должна быть небазисной, т.е. нулевой. Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений. Алгоритм симплекс-метода всегда начинается с некоторого допустимого базисного решения и затем пытается найти другое допустимое базисное решение, "улучшающее" значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в небазисные. Это необходимо, чтобы новое решение содержало в точности m базисных переменных. В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная — исключаемой (из базиса). Два правила выбора вводимых и исключающих переменных в симплекс-методе назовем условием оптимальности и условием допустимости. Сформулируем эти правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода. Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в z-строке. Если в z-строке есть несколько таких коэффициентов, то выбор вводимой переменной делается произвольно. Оптимальное решение достигнуто тогда, когда в z-строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными). Условие допустимости. Как в задаче максимизации, так и в задаче минимизации в качестве исключаемой выбирается базисная переменная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.
|

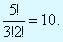 По определению базисное решение включает только две переменные, предполагая, что небазисных нулевых переменных три.
По определению базисное решение включает только две переменные, предполагая, что небазисных нулевых переменных три.


