Пример 4
Вступ. Розділ 1. Поняття, форми та значення працевлаштування. Розділ 2. Повноваження державної служби зайнятості з працевлаштування громадян. Розділ 3. Правовий статус безробітного. Висновки. Список використаної літератури. Додатки.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Справочный материал и пособие к практическим занятиям и СРС для студентов 1 и 2 курсов всех специальностей и форм обучения
Ø Первообразная и неопределённый интеграл Функция F(x) называется первообразной для функции f(x) на (a,b), если F/(x)=f(x) на (a,b). Множество всех первообразных для функции f(x) называется неопределенным интегралом и обозначается Основные свойства неопределенного интеграла 1. 2. 3. 4. 5. 6. Если 7. Если x=x(t) непрерывно дифференцируемая функция, то Таблица 1 Таблица простейших часто встречающихся интегралов 1. 3. 5. 7. 9. 11. 13. 15. 17. При применении свойств 6 и 7 полезно использовать табл. 2. Таблица 2 Таблица основных дифференциалов 1. 2. 3. 4. 5. 6. 7. 8.
Рассмотрим примеры нахождения неопределенного интеграла методом «подведения под знак дифференциала», т.е. будем использовать табл. 2. Пример 1
Пример 2
Пример 3
Пример 4
Ø Интегрирование путем замены переменной Один из наиболее распространенных методов, применяемых при вычислении неопределенных интегралов, метод замены переменных или подстановки. Если известно, что
Способ подстановки состоит в том, что сообразно виду подынтегральной функции составляют вспомогательную функцию, подстановка которой в исходный интеграл приводит его к виду более удобному для интегрирования (часто табличному). Рассмотрим примеры, уже решенные ранее:
|

 .
.
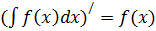




 .
. 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 

 18.
18. 

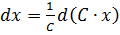
 где С-константа.
где С-константа.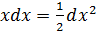 9.
9. 
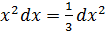 10.
10. 
 11.
11. 
 12.
12. 
 13.
13. 
 14.
14. 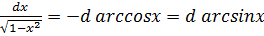
 15.
15. 
 .
.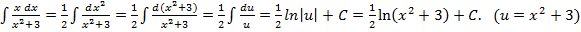 .
. .
. .
.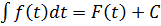 , то
, то где f(t), u(x), u/ (x) – непрерывны.
где f(t), u(x), u/ (x) – непрерывны. .
.


