Пример 11
Т.к
Других удобных значений X у нас нет. Применим метод сравнения коэффициентов при одинаковых степенях X в левой и правой частях.
Имеем
Ø Необходимые сведения и формулы Формулы сокращенного умножения
Выделение полного квадрата
Разложение квадратного трехчлена на множители
где
Тригонометрические формулы ü Функции одного угла
ü Функции кратных углов
ü Функции половинного угла
ü Произведение функций
ü Универсальная тригонометрическая подстановка
Гиперболические функции
Основные формулы гиперболической тригонометрии
Таблица производных элементарных функций
Правила дифференцирования
Производная сложной функции (функции от функции - цепное правило)
В случае длинной цепочки поступают аналогично.
Свойства дифференциала
|
.
-> m < n дробь правильная.
–> разложили как сумму кубов
.
.
имеет действительный корень х=-1 (х+1=0), то применим метод частных значений: подставим х=-1 в левую и правую часть разложения 
.
−> A=2.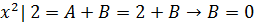
.
.
.
.
.
.
.
.
.
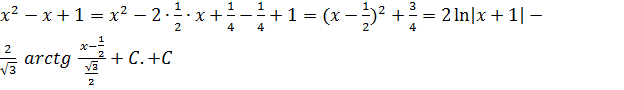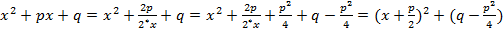, далее учесть, что 
, 
.
.
- корни квадратного трехчлена
, 
, если коэффициент b-четный, то удобнее использовать следующую формулу:
.
; 
; 
, 
; 
; 
.
; 
; 
.
; 
.
;
;
.
; 
.
; 
; 
.
; 
; 
.
; 
; 
; 
.
; 
; 
; 
, 
, 
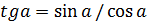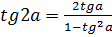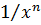
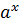
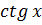
, где С-константа.
