Применение OpenGL. Описание примитивов вывода отрезков.

Работа по вычислению координат вектора при его повороте вокруг произвольный оси на произвольный угол выполняется в методе Rotate класса Point3D. В этом методе запрограммирована последняя формула. Важно не забыть перевести угол в радианы и нормировать вектор оси вращения, так как орт k в формуле имеет единичную длину, а входной параметр метода Rotate — нет.

class Point3D

{

public:

double x, y, z;

 

Point3D() { x = y = z = 0.; }

Point3D (double xx, double yy, double zz) { x = xx; y = yy; z = zz; }

Point3D (double v[3]) { x = v[0]; y = v[1]; z = v[2]; }

Point3D operator+ (Point3D& p) { return Point3D (x+p.x, y+p.y, z+p.z); }

Point3D operator- (Point3D& p) { return Point3D (x-p.x, y-p.y, z-p.z); }

void operator+= (Point3D& p) { x += p.x; y += p.y; z += p.z; }

void operator-= (Point3D& p) { x -= p.x; y -= p.y; z -= p.z; }

double operator! () { return sqrt (x*x + y*y + z*z); }

Point3D operator* (double d) { return Point3D (x*d, y*d, z*d); }

Point3D operator* (Point3D& p)

{

return Point3D (y*p.z - z*p.y, z*p.x - x*p.z, x*p.y - y*p.x);

}

 

void ToUnit ()

{

double r =!*this;

if (r!= 0)

{

x /= r; y /= r; z /= r;

}

}

 

double Dist (Point3D& p) { return!Point3D (*this - p); }

 

Point3D& Rotate (Point3D& p, double a)

{

a = a * ToRad;

p.ToUnit();

double

ca = cos(a),

sa = sin(a),

c = 1 - cos(a),

xs = p.x * sa,

ys = p.y * sa,

zs = p.z * sa,

xy = p.x * p.y * c,

xz = p.x * p.z * c,

yz = p.y * p.z * c,

xn = (p.x * p.x * c + ca) * x + (xy - zs) * y + (xz + ys) * z,

yn = (xy + zs) * x + (p.y * p.y * c + ca) * y + (yz - xs) * z,

zn = (xz - ys) * x + (yz + xs) * y + (p.z * p.z * c + ca) * z;

x = xn; y = yn; z = zn;

return *this;

}

};

Приведем пример вызова метода Rotate при вычислении нового положения вектора gU (объекта класса Point3D) при изменении угла крена angle в программе по управлению полетом.

gU.Rotate (gC - gE, angle);

Здесь gU, gC и gE являются веторами (объектами класса Point3D). Вектор gU необходимо повернуть при изменении угла крена модели летательного аппарата. При вызове функции OpenGL glLookAt, управляющей матрицей моделирования OpenGL, как вы помните, следует задать координаты трех векторов:

· Положение камеры (глаза наблюдателя) — gE,

· Положение центра сцены (точки, куда направлена камера) — gC,

· Направление вверх gU, которое должно быть ортогонально вектору направления взгляда (gC – gE).

Разность векторов gC и gE задает направление оси вращения, как видно из рисунка ниже.

gU

gC – gE

gE

o

k

angle

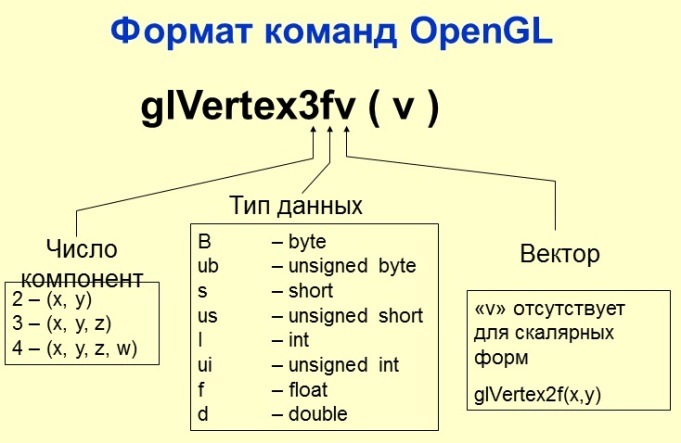
Полный текст программы, моделирующей полет (Pilot3.cpp и Pilot3M.cpp), приведен в папке с материалами курса. Для размышления о повороте векторов приведу код метода, который реализует изменение угла тангажа (Pitch). Угол поворота задается в градусах, поэтому он может быть целочисленным.

void Pitch (int angle)

{

Point3D

v = gC - gE, // Направление на центр сцены (взгляда)

n = v * gU; // Векторное произведение этих векторов определяет ось вращения при изменении тангажа

gC = gE + v.Rotate(n, angle);

gU.Rotate (n, angle);

Fly();

}

Обратите внимание, что при изменении угла тангажа (атаки) изменяется как положение центра сцены, так и направление вверх, которое должно всегда быть ортогональным направлению взляда.

Применение OpenGL. Описание общей структуры команд о OpenGL.

Применение OpenGL. Описание примитивов вывода отрезков.

GL_LINES	каждая отдельная пара вершин определяет отрезок; если задано нечетное число вершин, то последняя вершина игнорируется.
GL_LINE_STRIP	каждая следующая вершина задает отрезок вместе с предыдущей.
GL_LINE_LOOP	отличие от предыдущего примитива только в том, что последний отрезок определяется последней и первой вершиной, образуя замкнутую ломаную.