Обчисліть потрійний інтеграл  . Підінтегральна функція
. Підінтегральна функція  та поверхні, що обмежують область V, вказані в таблиці 1.
та поверхні, що обмежують область V, вказані в таблиці 1.
Таблиця 1.
| №
| 
| Область V
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 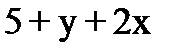
|  . .
|
|
| 
| 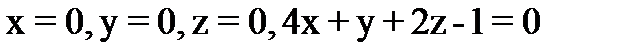 . .
|
|
| 
|  . .
|
|
| 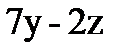
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 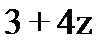
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
| 
|
|
| 
|  . .
|
|
| 
| 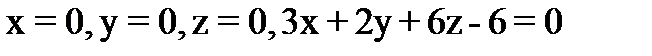 . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
| 
|
|
| 
|  . .
|
|
| 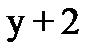
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 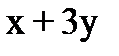
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
|
| 
|  . .
|
3.1. Обчисліть криволінійні інтеграли першого роду.
3.1.1.  , якщо
, якщо 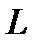 – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.1.2. 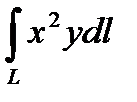 , якщо
, якщо  – чверть кола
– чверть кола  ,
,  ,
,  .
.
3.1.3.  , де
, де  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.1.4.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.1.5.  , якщо
, якщо  – дуга кривої
– дуга кривої 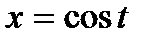 ,
,  ,
,  ,
,  .
.
3.1.6. 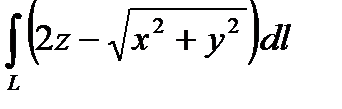 , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.1.7.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.8.  , де
, де  – відрізок прямої між точками
– відрізок прямої між точками  і
і  .
.
3.1.9.  , де
, де  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.1.10. 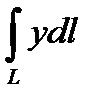 , де
, де  – дуга параболи
– дуга параболи  , яка міститься всередині параболи
, яка міститься всередині параболи  .
.
3.1.11.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.12.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
, 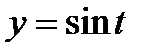 ,
,  ,
,  .
.
3.1.13. 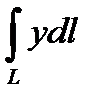 , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.14.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.15. 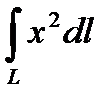 , якщо
, якщо  – дуга кривої
– дуга кривої  від точки
від точки 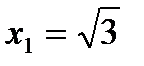 до точки
до точки  .
.
3.1.16.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  .
.
3.1.17.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.18.  , якщо
, якщо  – дуга кола
– дуга кола  ,
, 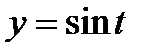 ,
,  .
.
3.1.19.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.20.  , якщо
, якщо  – дуга кривої
– дуга кривої 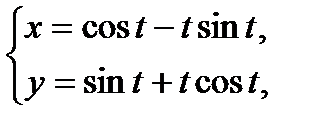
 .
.
3.1.21.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  .
.
3.1.22. 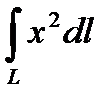 , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
, 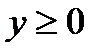 .
.
3.1.23. Обчисліть  , де
, де  – відрізок, що сполучає точки
– відрізок, що сполучає точки  і
і  .
.
3.1.24.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.25.  , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
.
3.1.26.  , якщо
, якщо  – дуга астроїди
– дуга астроїди  ,
,  ,
,  .
.
3.1.27.  , якщо
, якщо  – дуга кривої
– дуга кривої 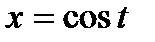 ,
,  ,
,  ,
, 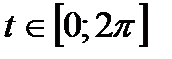 .
.
3.1.28.  , якщо
, якщо  – дуга кривої
– дуга кривої 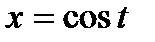 ,
,  ,
,  ,
,  .
.
3.1.29.  , якщо
, якщо  – дуга астроїди
– дуга астроїди  ,
,  ,
, 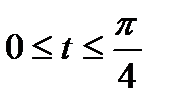 .
.
3.1.30.  , якщо
, якщо  – дуга кола
– дуга кола  ,
,  ,
,  .
.
3.2. Обчисліть криволінійні інтеграли другого роду (інтегрування проведіть у додатному напрямку).
3.2.1.  , якщо
, якщо  – дуга кривої
– дуга кривої 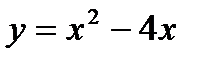 , розміщеної під віссю
, розміщеної під віссю  .
.
3.2.2.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
, 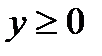 .
.
3.2.3.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.
3.2.4.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
, 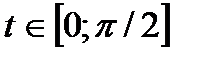 .
.
3.2.5.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  .
.
3.2.6.  , якщо
, якщо  – дуга параболи
– дуга параболи  ,
,  .
.
3.2.7. 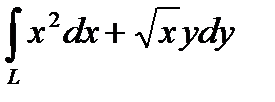 , якщо
, якщо  – чверть кола
– чверть кола  ,
,  ,
,  , що пробігається проти годинникової стрілки.
, що пробігається проти годинникової стрілки.
3.2.8.  , де
, де  – дуга кубічної параболи
– дуга кубічної параболи 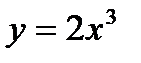 ,
,  .
.
3.2.9.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.10.  , якщо
, якщо  – дуга параболи
– дуга параболи  ,
,  .
.
3.2.11.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
, 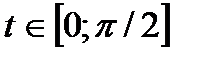 .
.
3.2.12.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  .
.
3.2.13.  , якщо
, якщо  – дуга параболи
– дуга параболи  ,
,  .
.
3.2.14.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  .
.
3.2.15.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.16.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.17.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.18.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.19.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.20.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
.
3.2.21.  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і 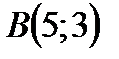 .
.
3.2.22.  якщо
якщо  – дуга параболи
– дуга параболи  , розміщеної над віссю
, розміщеної над віссю  .
.
3.2.23.  , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
.
3.2.24.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
, 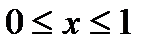 .
.
3.2.25.  , якщо
, якщо  – дуга параболи
– дуга параболи  ,
,  .
.
3.2.26.  , якщо
, якщо  – дуга кривої
– дуга кривої  ,
, 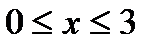 .
.
3.2.27.  , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
.
3.2.28.  , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
.
3.2.29.  , якщо
, якщо  – дуга параболи
– дуга параболи  ,
, 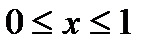
3.2.30.  , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки 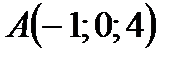 і
і  .
.
3.3. Обчисліть криволінійний інтеграл  по замкненому контуру L, використовуючи формулу Гріна. Обхід контура відбувається проти годинникової стрілки.
по замкненому контуру L, використовуючи формулу Гріна. Обхід контура відбувається проти годинникової стрілки.
3.3.1. 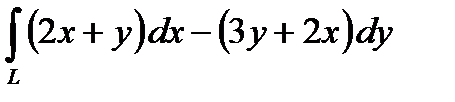 , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
, 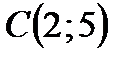 .
.
3.3.2.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.3.  , якщо
, якщо  – контур, обмежений параболою
– контур, обмежений параболою  і прямою
і прямою  .
.
3.3.4.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
, 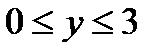
3.3.5.  , якщо
, якщо  – контур, обмежений параболами
– контур, обмежений параболами  і
і  .
.
3.3.6.  , якщо
, якщо  – контур прямокутника
– контур прямокутника 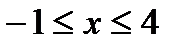 ,
, 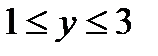
3.3.7.  , якщо
, якщо  – контур, обмежений параболою
– контур, обмежений параболою  і прямою
і прямою  .
.
3.3.8. 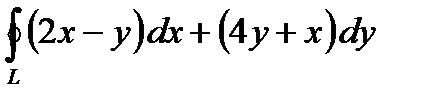 , де
, де  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
, 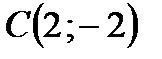 .
.
3.3.9.  , де
, де  – контур обмежений параболою
– контур обмежений параболою  і прямою
і прямою  .
.
3.3.10.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.11.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
, 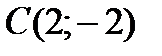 .
.
3.3.12.  , якщо
, якщо  – коло
– коло 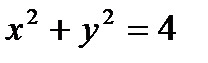
3.3.13.  , якщо
, якщо  – контур, обмежений параболою
– контур, обмежений параболою  і прямою
і прямою  .
.
3.3.14. 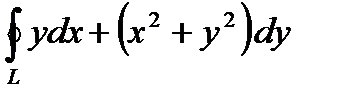 , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.15.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
,  .
.
3.3.16.  , якщо
, якщо  – контур, утворений параболами
– контур, утворений параболами  та
та  .
.
3.3.17.  , якщо
, якщо  – коло
– коло  .
.
3.3.18. 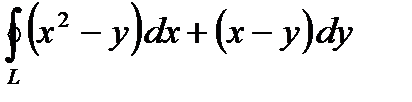 , якщо
, якщо  – контур, утворений параболою
– контур, утворений параболою  та прямою
та прямою  .
.
3.3.19.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.20.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.21.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
,  .
.
3.3.22.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.23.  , якщо
, якщо  – контур, утворений параболою
– контур, утворений параболою  та прямою
та прямою  .
.
3.3.24.  , якщо
, якщо  – коло
– коло  .
.
3.3.25.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
,  .
.
3.3.26.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
,  .
.
3.3.27.  , якщо
, якщо  – контур, обмежений параболами
– контур, обмежений параболами  та
та 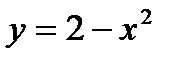 .
.
3.3.28.  , якщо
, якщо  – контур прямокутника
– контур прямокутника  ,
,  .
.
3.3.29.  , якщо
, якщо  – коло
– коло  .
.
3.3.30.  , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
, 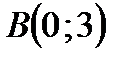 ,
,  .
.
3.4. Перевірте, що криволінійний інтеграл не залежить від форми шляху інтегрування та обчисліть його.
3.4.1.  .
.
3.4.2.  .
.
3.4.3.  .
.
3.4.4.  .
.
3.4.5.  .
.
3.4.6.  .
.
3.4.7.  .
.
3.4.8.  .
.
3.4.9.  .
.
3.4.10. 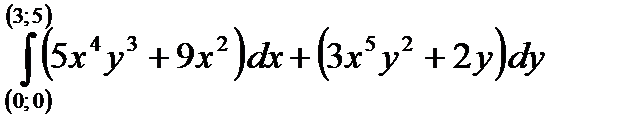 .
.
3.4.11.  .
.
3.4.12.  .
.
3.4.13. 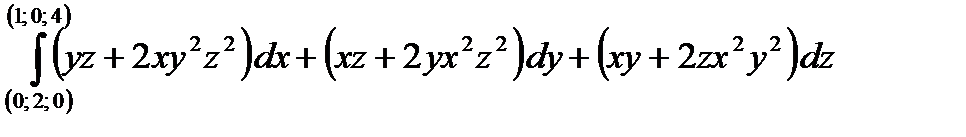 .
.
3.4.14.  .
.
3.4.15.  .
.
3.4.16.  .
.
3.4.17.  .
.
3.4.18.  .
.
3.4.19.  .
.
3.4.20.  .
.
3.4.21.  .
.
3.4.22.  .
.
3.4.23.  .
.
3.4.24.  .
.
3.4.25.  .
.
3.4.26.  .
.
3.4.27.  .
.
3.4.28.  .
.
3.4.29.  .
.
3.4.30.  .
.
5.1. Обчисліть потік вектора  через зовнішню поверхню піраміди, що обмежена координатними площинами
через зовнішню поверхню піраміди, що обмежена координатними площинами  та похилою площиною
та похилою площиною  , користуючись формулою Остроградського – Гаусса.
, користуючись формулою Остроградського – Гаусса.
| №
| 
| Рівняння площини 
|
| 5.1.1
| 
| 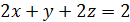
|
| 5.1.2
| 
| 
|
| 5.1.3
| 
| 
|
| 5.1.4
| 
| 
|
| 5.1.5
| 
| 
|
| 5.1.6
| 
| 
|
| 5.1.7
| 
| 
|
| 5.1.8
| 
| 
|
| 5.1.9
| 
| 
|
| 5.1.10
| 
| 
|
| 5.1.11
| 
| 
|
| 5.1.12
| 
| 
|
| 5.1.13
| 
| 
|
| 5.1.14
| 
| 
|
| 5.1.15
| 
| 
|
| 5.1.16
| 
| 
|
| 5.1.17
| 
| 
|
| 5.1.18
| 
| 
|
| 5.1.19
| 
| 
|
| 5.1.20
| 
| 
|
| 5.1.21
| 
| 
|
| 5.1.22
| 
| 
|
| 5.1.23
| 
| 
|
| 5.1.24
| 
| 
|
| 5.1.25
| 
| 
|
| 5.1.26
| 
| 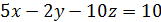
|
| 5.1.27
| 
| 
|
| 5.1.28
| 
| 
|
| 5.1.29
| 
| 
|
| 5.1.30
| 
| 
|
5.2. Обчисліть циркуляцію векторного поля 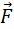 вздовж лінії перетину площини
вздовж лінії перетину площини  з координатними площинами, використовуючи безпосереднє обчислення та формулу Стокса (напрям руху вздовж кривої відбувається проти годинникової стрілки, якщо дивитися з початку координат).
з координатними площинами, використовуючи безпосереднє обчислення та формулу Стокса (напрям руху вздовж кривої відбувається проти годинникової стрілки, якщо дивитися з початку координат).
5.2.1. 
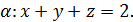
5.2.2. 
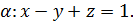
5.2.3. 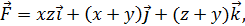

5.2.4. 
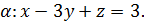
5.2.5. 

5.2.6. 
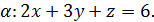
5.2.7. 

5.2.8. 
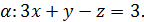
5.2.9. 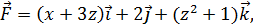
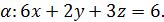
5.2.10. 
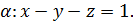
5.2.11. 
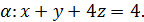
5.2.12. 
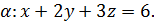
5.2.13. 
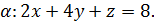
5.2.14. 
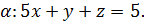
5.2.15. 

Обчисліть циркуляцію векторного поля  вздовж замкненої лінії L двома способами (безпосередньо та за формулою Стокса).
вздовж замкненої лінії L двома способами (безпосередньо та за формулою Стокса).
5.2.16. 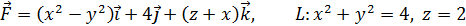 .
.
5.2.17.  .
.
5.2.18. 
5.2.19.  .
.
5.2.20.  .
.
5.2.21. 
5.2.22.  .
.
5.2.23.  .
.
5.2.24. 
5.2.25.  .
.
5.2.26. 
5.2.27. 
5.2.28. 
5.2.29. 

 . Підінтегральна функція
. Підінтегральна функція  та поверхні, що обмежують область V, вказані в таблиці 1.
та поверхні, що обмежують область V, вказані в таблиці 1.
 .
.

 .
.
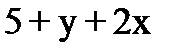
 .
.

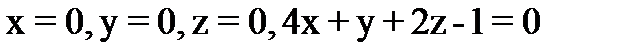 .
.

 .
.
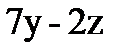
 .
.

 .
.

 .
.

 .
.
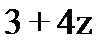
 .
.

 .
.

 .
.



 .
.

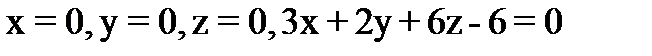 .
.

 .
.

 .
.

 .
.

 .
.

 .
.



 .
.
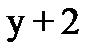
 .
.

 .
.

 .
.

 .
.
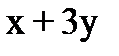
 .
.

 .
.

 .
.

 .
.
 , якщо
, якщо 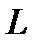 – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.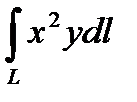 , якщо
, якщо  – чверть кола
– чверть кола  ,
,  ,
,  .
. , де
, де  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
. , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
. , якщо
, якщо  – дуга кривої
– дуга кривої 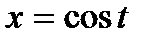 ,
,  ,
,  ,
,  .
.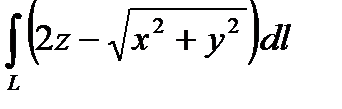 , якщо
, якщо  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
. , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
. , де
, де  – відрізок прямої між точками
– відрізок прямої між точками  і
і  .
. , де
, де  – дуга кривої
– дуга кривої  ,
,  ,
,  ,
,  .
.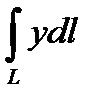 , де
, де  – дуга параболи
– дуга параболи  , яка міститься всередині параболи
, яка міститься всередині параболи  .
. , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
. , якщо
, якщо  – дуга кривої
– дуга кривої  ,
, 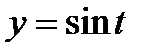 ,
,  ,
,  .
.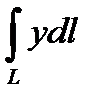 , якщо
, якщо  – дуга кривої
– дуга кривої 
 .
. , якщо
, якщо 
 .
.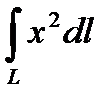 , якщо
, якщо  від точки
від точки 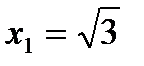 до точки
до точки  .
. , якщо
, якщо  ,
,  ,
,  .
. , якщо
, якщо 
 .
. .
.
 .
.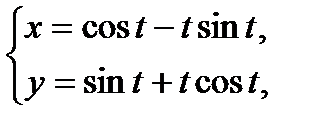
 ,
,  ,
,  .
. ,
,  ,
, 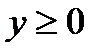 .
. , де
, де  – відрізок, що сполучає точки
– відрізок, що сполучає точки  і
і  .
. , якщо
, якщо 

 , якщо
, якщо  ,
,  ,
,  .
. , якщо
, якщо 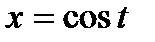 ,
,  ,
,  ,
, 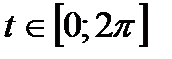 .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо 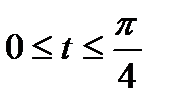 .
. ,
,  ,
,  .
. , якщо
, якщо 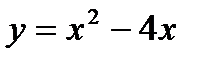 , розміщеної під віссю
, розміщеної під віссю  .
. , якщо
, якщо  ,
,  ,
, 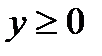 .
. , якщо
, якщо  ,
,  ,
,  ,
,  , якщо
, якщо  ,
,  ,
, 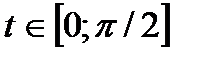 .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  .
.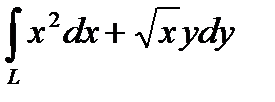 , якщо
, якщо  ,
,  ,
,  , що пробігається проти годинникової стрілки.
, що пробігається проти годинникової стрілки. , де
, де 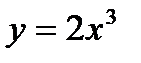 ,
,  , якщо
, якщо  – відрізок прямої, що сполучає точки
– відрізок прямої, що сполучає точки  і
і  .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  , якщо
, якщо  ,
,  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і  .
. , якщо
, якщо  і
і 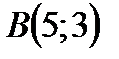 .
. якщо
якщо  , розміщеної над віссю
, розміщеної над віссю  .
. , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
. , якщо
, якщо  ,
, 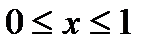 .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
, 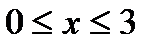 .
. , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
. , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки  і
і  .
. , якщо
, якщо  ,
, 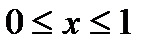
 , якщо АВ – відрізок прямої, що сполучає точки
, якщо АВ – відрізок прямої, що сполучає точки 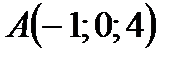 і
і  .
. по замкненому контуру L, використовуючи формулу Гріна. Обхід контура відбувається проти годинникової стрілки.
по замкненому контуру L, використовуючи формулу Гріна. Обхід контура відбувається проти годинникової стрілки.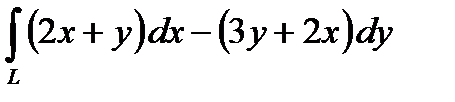 , якщо
, якщо  – контур трикутника з вершинами
– контур трикутника з вершинами  ,
,  ,
, 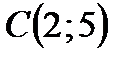 .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  і прямою
і прямою  .
. , якщо
, якщо  ,
, 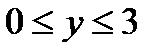
 , якщо
, якщо  і
і  .
. , якщо
, якщо 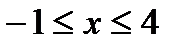 ,
, 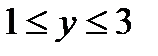
 , якщо
, якщо  .
.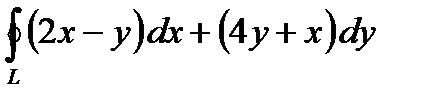 , де
, де  ,
,  ,
, 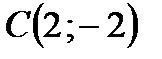 .
. , де
, де  і прямою
і прямою  .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  ,
, 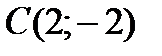 .
. , якщо
, якщо 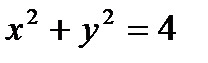
 , якщо
, якщо  і прямою
і прямою  .
.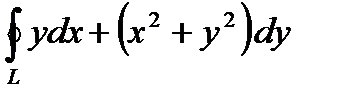 , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  ,
,  .
. , якщо
, якщо  та
та  .
. , якщо
, якщо  .
.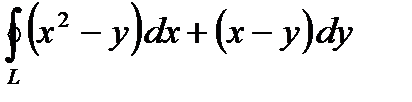 , якщо
, якщо  та прямою
та прямою  .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  ,
,  ,
,  .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  та прямою
та прямою  .
. , якщо
, якщо  .
. , якщо
, якщо  ,
,  , якщо
, якщо  ,
,  ,
,  .
. , якщо
, якщо 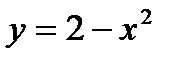 .
. , якщо
, якщо  ,
,  .
. , якщо
, якщо  .
. , якщо
, якщо  ,
, 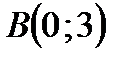 ,
,  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.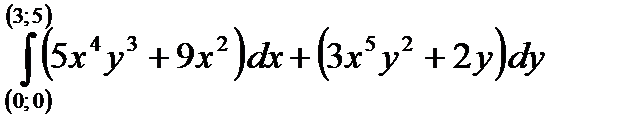 .
. .
. .
.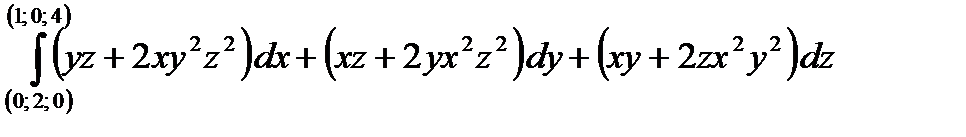 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. через зовнішню поверхню піраміди, що обмежена координатними площинами
через зовнішню поверхню піраміди, що обмежена координатними площинами  та похилою площиною
та похилою площиною  , користуючись формулою Остроградського – Гаусса.
, користуючись формулою Остроградського – Гаусса.


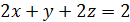














































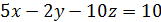








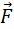 вздовж лінії перетину площини
вздовж лінії перетину площини 
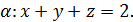

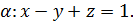
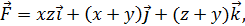


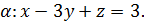



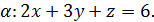



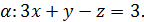
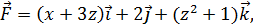
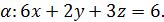

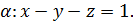

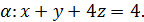

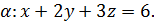

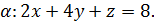

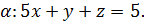


 вздовж замкненої лінії L двома способами (безпосередньо та за формулою Стокса).
вздовж замкненої лінії L двома способами (безпосередньо та за формулою Стокса).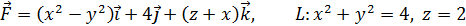 .
. .
.
 .
. .
.
 .
. .
.
 .
.





