Известны (рис.3.1,а) ток нагрузки  , напряжение в конце линии
, напряжение в конце линии  , сопротивление и проводимость линии
, сопротивление и проводимость линии  ,
,  . Определим напряжение в начале линии
. Определим напряжение в начале линии  , ток в продольной части линии
, ток в продольной части линии  , потери мощности в линии
, потери мощности в линии  и ток
и ток  .
.
Расчет линии электропередачи состоит в определении неизвестных токов и напряжений последовательно от конца линии к началу. Для определения токов и напряжений применяются первый закон Кирхгофа и закон Ома.
 Рис.3.1 Установившийся режим линии электропередачи:
Рис.3.1 Установившийся режим линии электропередачи:
а) схема замещения; б) определение емкостного тока.
Используем фазные напряжения  и токи
и токи  . Емкостный ток в конце линии 12, соединяющий узлы 1 и 2, по закону Ома (рис.3.1,б)
. Емкостный ток в конце линии 12, соединяющий узлы 1 и 2, по закону Ома (рис.3.1,б)
 . (3.1)
. (3.1)
Ток в продольной части линии 12 по первому закону Кирхгофа
 . (3.2)
. (3.2)
Напряжение в начале линии по закону Ома
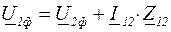 . (3.3)
. (3.3)
Емкостный ток в начале линии
 . (3.4)
. (3.4)
Ток в начале линии по первому закону Кирхгофа
 . (3.5)
. (3.5)
Потери мощности в линии (в трех фазах)
 . (3.6)
. (3.6)
Векторная диаграмма токов и напряжений для линии с нагрузкой (рис.3.2,а) строится в соответствии с выражениями (3.1)-(3.5). Вначале строим на диаграмме известные  и
и  . Полагаем, что
. Полагаем, что  , т.е. напряжение
, т.е. напряжение  направлено по действительной оси. Емкостный ток
направлено по действительной оси. Емкостный ток  опережает на 90о напряжение
опережает на 90о напряжение  . Ток
. Ток  соединяет начало первого и конец второго суммируемых векторов в правой части (3.2). Затем строим отдельно два слагаемых в правой части (3.3):
соединяет начало первого и конец второго суммируемых векторов в правой части (3.2). Затем строим отдельно два слагаемых в правой части (3.3):
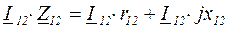 . (3.7)
. (3.7)


Рис.3.2 Векторные диаграммы токов и напряжений линии
электропередачи: а) линия с нагрузкой; б) линия
на холостом ходу.
Вектор  параллелен
параллелен  . Вектор
. Вектор  опережает на 90о ток
опережает на 90о ток  . Напряжение
. Напряжение  соединяет начало и конец суммируемых векторов
соединяет начало и конец суммируемых векторов  . Ток
. Ток  опережает
опережает  на 90о,
на 90о,  соответствует (3.5). В линии с нагрузкой напряжение в конце по модулю меньше, чем в начале,
соответствует (3.5). В линии с нагрузкой напряжение в конце по модулю меньше, чем в начале,  (рис.3.1).
(рис.3.1).
В линии на холостом ходу, т.е. при токе нагрузки  , течет только емкостный ток, так как в соответствии с (3.2)
, течет только емкостный ток, так как в соответствии с (3.2)
 . (3.8)
. (3.8)
В этом случае напряжение в конце линии повышается:  . Векторная диаграмма токов и напряжений для такой линии приведена на рис.3.2,б.
. Векторная диаграмма токов и напряжений для такой линии приведена на рис.3.2,б.

 , напряжение в конце линии
, напряжение в конце линии  , сопротивление и проводимость линии
, сопротивление и проводимость линии  ,
,  . Определим напряжение в начале линии
. Определим напряжение в начале линии  , ток в продольной части линии
, ток в продольной части линии  , потери мощности в линии
, потери мощности в линии  и ток
и ток  .
. Рис.3.1 Установившийся режим линии электропередачи:
Рис.3.1 Установившийся режим линии электропередачи: и токи
и токи  . Емкостный ток в конце линии 12, соединяющий узлы 1 и 2, по закону Ома (рис.3.1,б)
. Емкостный ток в конце линии 12, соединяющий узлы 1 и 2, по закону Ома (рис.3.1,б) . (3.1)
. (3.1) . (3.2)
. (3.2)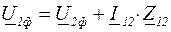 . (3.3)
. (3.3) . (3.4)
. (3.4) . (3.5)
. (3.5) . (3.6)
. (3.6) и
и  , т.е. напряжение
, т.е. напряжение  опережает на 90о напряжение
опережает на 90о напряжение 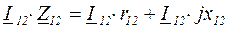 . (3.7)
. (3.7)

 параллелен
параллелен  опережает на 90о ток
опережает на 90о ток  соединяет начало и конец суммируемых векторов
соединяет начало и конец суммируемых векторов  . Ток
. Ток  опережает
опережает  (рис.3.1).
(рис.3.1). , течет только емкостный ток, так как в соответствии с (3.2)
, течет только емкостный ток, так как в соответствии с (3.2) . (3.8)
. (3.8) . Векторная диаграмма токов и напряжений для такой линии приведена на рис.3.2,б.
. Векторная диаграмма токов и напряжений для такой линии приведена на рис.3.2,б.


