Учитывая, что полупроводник собственный, то есть: n 0 = p 0 = ni и  и
и 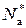 = 0.
= 0.
И заменив электростатический потенциал φ Е на –φ, плотность заряда приведется к виду
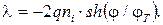 (2.41)
(2.41)
Подставим полученное значение λ в правую часть (2.38), поделим обе части на φ Т и введем безразмерную переменную Ф = φ/φ Т. После этого уравнение Пуассона примет вид:
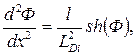 (2.42)
где (2.42)
где 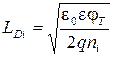 дебаевская длина в собственном полупроводнике (2.43).
Для кремния LDi = 14 мкм.
l – глубина проникновения зарядов.
Рассмотрим простейший случай, когда |φs| < φ Т, т.e. |Φ|<1. В этом случае можно положить sh Ф ≈ Ф и (2.42) превращается в линейное дифференциальное уравнение 1-го порядка. Для граничных условий φ(∞) = 0 и φ(0) = φs, решение имеет вид: дебаевская длина в собственном полупроводнике (2.43).
Для кремния LDi = 14 мкм.
l – глубина проникновения зарядов.
Рассмотрим простейший случай, когда |φs| < φ Т, т.e. |Φ|<1. В этом случае можно положить sh Ф ≈ Ф и (2.42) превращается в линейное дифференциальное уравнение 1-го порядка. Для граничных условий φ(∞) = 0 и φ(0) = φs, решение имеет вид:
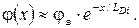 (2.44)
Из (2.44) следует, что дебаевская длина — это расстояние, на котором потенциал уменьшается в е раз по сравнению с максимальным значением φ( x ) на поверхности. (2.44)
Из (2.44) следует, что дебаевская длина — это расстояние, на котором потенциал уменьшается в е раз по сравнению с максимальным значением φ( x ) на поверхности.
| 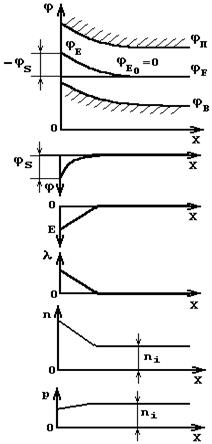 Рис.2.14. Эффект поля в собственном полупроводнике:
зонная диаграмма, распределение потенциала, поля, заряда и концентраций носителей
Рис.2.14. Эффект поля в собственном полупроводнике:
зонная диаграмма, распределение потенциала, поля, заряда и концентраций носителей
|
На рис. 2.14 для той же полярности напряжения, что и на рис. 2.13, показана зонная диаграмма, распределение потенциала, поля, заряда и концентраций носителей.
Искривление энергетических зон вблизи границы полупроводник-диэлектрик — характерная особенность эффекта поля.
Если изменить полярность напряжения, то знак объемного заряда изменится и зоны искривятся в другую сторону — «вниз». Однако при обеих полярностях приповерхностный слой в собственном полупроводнике оказывается обогащенным (либо электронами, либо дырками).
Величину поверхностного потенциала можно найти из условия непрерывности электрической индукции на границе полупроводник-диэлектрик:
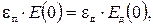 (2.45)
(2.45)
где εп и εд — относительные диэлектрические проницаемости полупроводника и диэлектрика.
Поле в диэлектрике постоянное, поэтому (рис. 2.13)
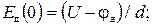 (2.46)
(2.46)
поле в полупроводнике на границе с диэлектриком (рис. 2.14)определяется функцией φ(х):
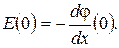 (2.47)
(2.47)
Зависимость φs(U) показана в виде кривых на рис. 2.15
| Из этих кривых видно, что поверхностный потенциал составляет тем большую долю приложенного напряжения, чем тоньше диэлектрик (чем меньше параметр a). При всех реальных значениях толщины диэлектрика и приложенного напряжения поверхностный потенциал не превышает нескольких десятых долей вольта.
| 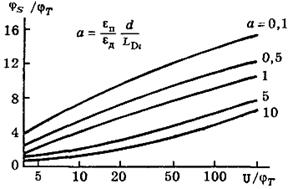 Рис. 2.15. Зависимость поверхностного потенциала в собственном полупроводнике от толщины диэлектрика и напряжения на металлическом электроде
Рис. 2.15. Зависимость поверхностного потенциала в собственном полупроводнике от толщины диэлектрика и напряжения на металлическом электроде
|

 и
и 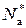 = 0.
= 0.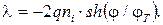 (2.41)
(2.41)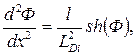 (2.42)
где
(2.42)
где 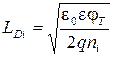 дебаевская длина в собственном полупроводнике (2.43).
Для кремния LDi = 14 мкм.
l – глубина проникновения зарядов.
Рассмотрим простейший случай, когда |φs| < φ Т, т.e. |Φ|<1. В этом случае можно положить sh Ф ≈ Ф и (2.42) превращается в линейное дифференциальное уравнение 1-го порядка. Для граничных условий φ(∞) = 0 и φ(0) = φs, решение имеет вид:
дебаевская длина в собственном полупроводнике (2.43).
Для кремния LDi = 14 мкм.
l – глубина проникновения зарядов.
Рассмотрим простейший случай, когда |φs| < φ Т, т.e. |Φ|<1. В этом случае можно положить sh Ф ≈ Ф и (2.42) превращается в линейное дифференциальное уравнение 1-го порядка. Для граничных условий φ(∞) = 0 и φ(0) = φs, решение имеет вид:
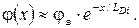 (2.44)
Из (2.44) следует, что дебаевская длина — это расстояние, на котором потенциал уменьшается в е раз по сравнению с максимальным значением φ( x ) на поверхности.
(2.44)
Из (2.44) следует, что дебаевская длина — это расстояние, на котором потенциал уменьшается в е раз по сравнению с максимальным значением φ( x ) на поверхности.
 Рис.2.14. Эффект поля в собственном полупроводнике:
зонная диаграмма, распределение потенциала, поля, заряда и концентраций носителей
Рис.2.14. Эффект поля в собственном полупроводнике:
зонная диаграмма, распределение потенциала, поля, заряда и концентраций носителей
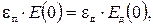 (2.45)
(2.45)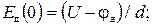 (2.46)
(2.46)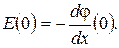 (2.47)
(2.47) Рис. 2.15. Зависимость поверхностного потенциала в собственном полупроводнике от толщины диэлектрика и напряжения на металлическом электроде
Рис. 2.15. Зависимость поверхностного потенциала в собственном полупроводнике от толщины диэлектрика и напряжения на металлическом электроде



