Законы движения носителей заряда в полупроводниках
В общем случае движение носителей заряда обусловлено двумя процессами: диффузией под действием градиента концентрации и дрейфом под действием градиента электрического потенциала. Поскольку имеются два типа носителей — электроны и дырки, полный ток состоит из четырех составляющих:
где индексы «др» и «диф» относятся соответственно к дрейфовым и диффузионным составляющим тока. При анализе удобнее пользоваться не токами, а плотностями токов j, что и сделано в формуле (2.29). Там, где это не вызывает недоразумений, будем для краткости называть величину j током. Составляющие тока. В одномерном случае, когда движение носителей происходит только вдоль оси х, дрейфовые составляющие записываются следующим образом:
где Е – напряженность электрического поля; U – потенциал. Тогда диффузионные составляющие токов запишутся следующим образом:
где Dn и Dp - коэффициенты диффузии электронов и дырок. Эти величины играют при диффузии ту же роль, что и подвижности при дрейфовом механизме движения. Связь между коэффициентами диффузии и подвижностями выражается формулой Эйнштейна:
Сравнивая выражения (2.30) и (2.31), можно заметить, что дрейфовые составляющие токов пропорциональны концентрациям носителей, тогда как диффузионные не зависят от концентраций, а определяются только градиентами концентрации. Диффузия носителей. Пусть на поверхность полупроводника падает рассеянный пучок света (рис. 2.9). Тогда в тонком приповерхностном слое, в который проникает свет, будут генерироваться электронно-дырочные пары. Между поверхностью и объемом возникнут градиенты концентрации электронов и дырок и избыточные носители начнут диффундировать вглубь полупроводника. Такое совместное движение обоих типов носителей называют биполярной или амбиполярной диффузией.
и ускоряет поток дырок. В конце концов устанавливается стационарный режим, при котором избыточные электроны и дырки распределены в виде сдвинутых относительно друг друга «облачков». Эти «облачка» двигаются синхронно, так что результирующий ток отсутствует. Концентрация носителей в «облачках» спадает с удалением от поверхности благодаря рекомбинации. Описанные явления известны под названием эффекта Дембера, а электрическое поле и разность потенциалов, свойственные этому эффекту, называют демберовским полем и демберовским напряжением. Эффект Дембера существенен только при больших избыточных концентрациях и больших удельных сопротивлениях полупроводников. На практике главную роль играет монополярная диффузия [4], характерная тем, что в приповерхностный слой полупроводника тем или иным способом вводится
электронно-дырочное «облачко», почти такое же, как при биполярной диффузии. Несмотря на это внешнее сходство, монополярная диффузия принципиально отличается от биполярной следующими особенностями: наличие тока предполагает, что полупроводник является элементом замкнутой цели; значит, помимо демберовского поля (сосредоточенного вблизи инжектирующей поверхности) во всей толще полупроводника действует «обычное» —омическое поле, обусловленное приложенным напряжением(рис. 2.10); потоки электронов и дырок направлены в разные стороны: электроны двигаются вглубь кристалла, а дырки в сторону инжектирующей поверхности — в район электронно-дырочного «облачка», где происходит интенсивная рекомбинация и необходимо пополнение основных носителей; в связи с постоянством полного тока его электронная и дырочная составляющие меняются в разные стороны: с удалением от поверхности электронный ток убывает (из-за рекомбинации), а дырочный ток растет; поэтому вдали от поверхности дырочная составляющая — главная и имеет чисто дрейфовый характер (дырки двигаются в поле, созданном внешним напряжением); наоборот, в непосредственной близости от поверхности ток почти чисто электронный и обусловлен диффузией, так как напряженность поля здесь близка к нулю (рис. 2.10). Величина L, называемая средней диффузионной длиной определяется выражением:
L характеризует то среднее расстояние, на которое носители успевают продиффундировать за время жизни. Поэтому отношение l /τ есть средняя скорость диффузии носителей. Диффузионная длина — одна из фундаментальных величин в полупроводниковой физике и технике. Для кремния типичные значения L составляют 5-20 мкм в зависимости от времени жизни. Распределение избыточной концентрации (рис. 2.11,а) примет вид:
Рис.2.11. Стационарное распределение избыточных носителей при инжекции (а) и экстракции (б)
Из этого выражения и из рис. 2.11, а следует, что на расстоянии диффузионной длины избыточная концентрация уменьшается в е раз. На участке длиной (3-4) L концентрация уменьшается в 20-50 раз, т.е. становится пренебрежимо малой по сравнению с граничной. Дифференцируя (2.34), получаем градиент концентрации
Как видим, градиент концентрации, а значит, и диффузионный ток спадают по мере удаления от поверхности вглубь кристалла. Градиент имеет максимальное (по модулю) значение при х = 0, т.е. на инжектирующей поверхности:
Качественные выводы относительно переходного процесса состоят в следующем. В начальный момент, когда L(0) = 0, градиент концентрации вблизи инжектирующей поверхности согласно (2.36) оказывается бесконечно большим, и, следовательно, избыточные носители будут диффундировать в кристалл с очень большой скоростью.
Рис.2.12. Распределение инжектированных носителей во время переходного процесса По мере нарастания величины L(t) градиент концентрации на поверхности уменьшается, и скорость диффузии становится все меньше. В конце концов при t ≈ 2τ достигается стационарный режим. Исходя из таких соображений, на рис. 2.12 показаны примерные кривые распределения концентрации для нескольких моментов переходного процесса. Концентрация неравновесных носителей будет убывать во времени и в пространстве по экспоненциальному закону
Величина 1/τ, обратная времени жизни носителей, будет характеризовать скорость рекомбинации. Скорость рекомбинации будет тем выше, чем выше концентрация основных носителей.
|

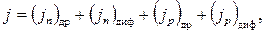 (2.29)
(2.29)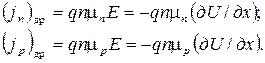 (2.30)
(2.30) (2.31)
(2.31)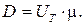 (2.32)
(2.32) Рис.2.9. Биполярная диффузия, эффект Дембера
Рис.2.9. Биполярная диффузия, эффект Дембера
 Рис.2.10. Монополярная диффузия;
инжекция носителей: 1 – омическое поле; 2- демберовское поле
Рис.2.10. Монополярная диффузия;
инжекция носителей: 1 – омическое поле; 2- демберовское поле
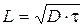 (2.33)
(2.33) (2.34)
(2.34)
 (2.35)
(2.35)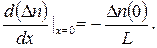 (2.36)
(2.36)

 (2.37)
(2.37)


