Энергия электрического поля. Плотность энергии.
Будем заряжать плоский конденсатор, перенося малые порции заряда dq с одной обкладки на другую (рис. 4.12.) Для того чтобы перенести заряд dq между обкладками с разностью потенциалов (j1 – j2) необходимо совершить работу dA = (j1 – j2) dq (4.11)
Рис. 4.12. Учитывая, что
Для того чтобы первоначально незаряженному конденсатору сообщить заряд Q, необходимо совершить работу
Эта работа равна энергии заряженного конденсатора
Здесь Продолжим преобразования уравнения (4.12). Вспомним, что ёмкость плоского конденсатора
а напряжение связано с напряжённостью электрического поля U = E ∙ d Воспользовавшись этими соотношениями, запишем энергию заряженного конденсатора в таком виде
Эти два выражения энергии конденсатора
приводят к следующему принципиальному вопросу: где в конденсаторе располагается энергия? Где она «локализована»? Если она связана с электрическими зарядами, то она находиться на обкладках конденсатора. Если же это энергия электрического поля, то она занимает пространство между обкладками, объем которого равен объему конденсатора V = S ∙ d. Для ответа на этот вопрос нужно было бы заряд с обкладок убрать, а поле при этом оставить. Тогда можно было бы посмотреть: осталась энергия — значит, она связана с полем, исчезла — значит, она располагалась вместе с зарядом на обкладках. Но проблема-то в том, что при удалении зарядов исчезает, конечно, и их электростатическое поле. Поэтому вопрос о локализации энергии в рамках электростатики не может быть решён. В электродинамике переменные электрические и магнитные поля, как известно, могут существовать и без электрических зарядов. Причем такие поля обладают энергией, что является прямым экспериментальным доказательством того, что эта энергия связана с электрическими полями и локализована в объёме, занятом полем. Теперь становиться понятнее последнее выражение энергии заряженного конденсатора:
Энергия конденсатора связана с его электрическим полем и поэтому пропорциональна объёму конденсатора (V), то есть объёму поля. Отношение Эта характеристика энергетической насыщённости поля получила название «объёмная плотность энергии». Обычно эта характеристика носит точечный, локальный характер. Вокруг заданной точки выбирают элементарный объём dV и вычисляют энергетическую плотность, деля энергию этой области dW на её объём
Объёмная плотность энергии в заданной точке электрического поля пропорциональна квадрату напряжённости поля в этой точке. Измеряется объёмная плотность энергии, конечно, в Дж/м3:
Зная, как меняется плотность энергии в пространстве, можно вычислить энергию, сосредоточенную в объёме V, электрического поля:
Пример. Проводящий шар радиусом R несет заряд Q. Какова энергия электрического поля этого шара? Поле внутри заряженного шара отсутствует, а вне шара оно совпадает с полем точечного заряда:
Объёмная плотность энергии такого поля
Вычислим энергию, сосредоточенную в сферическом слое толщиной dr (рис. 4.13.)
Рис. 4.13.
Теперь просуммируем энергии всех слоёв от R до ¥
Вспомним, что 4pe0 R = с — ёмкость шара (см. 4.4.), а
Эта энергия поля равна работе, которая была совершена при зарядке шара до потенциала j0 = Начнем заряжать шар, перенося на него из бесконечности электрические заряды малыми порциями dq. Если в некоторый момент времени заряд шара окажется равным q, а его потенциал —
Теперь легко вычислить полную работу, которую необходимо проделать, чтобы передать первоначально незаряженному шару заряд Q:
Эта работа, как и ожидалось, равна энергии электрического поля, созданного нами при зарядке шара (см. 4.15). Лекция 5 «Электрическое поле в диэлектриках» План лекции 1. Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации. 2. Диэлектрическая проницаемость. Вектор электрического смещения. 3. Законы электрического поля в диэлектриках. 3.1. Закон Кулона. 3.2. Теорема Остроградского-Гаусса. 4. Граничные условия для электрического поля на поверхности раздела двух диэлектриков.
На прошлой лекции рассматривалось явление электростатической индукции — разделение зарядов проводника в электрическом поле. Свободные заряды в проводнике перемещаются под действием внешнего поля до тех пор, пока результирующее электрическое поле внутри проводника не окажется равным нулю. В связи с этим говорят, что проводник «разрушает электрическое поле, низводя его напряжённость до нуля». Из школьного курса известно, что и диэлектрики оказывают заметное влияние на электрическое поле: напряжённость поля в диэлектрике уменьшается в e раз по сравнению с полем в вакууме Е 0: Такое влияние диэлектрика на электрическое поле обусловлено поляризацией диэлектрика. Явление поляризации и законы электрического поля в диэлектриках — тема настоящей лекции.
|


 , эту работу можно записать ещё и так
, эту работу можно записать ещё и так

 (4.12)
(4.12)
 — напряжение на конденсаторе, равное разности потенциалов на его обкладках.
— напряжение на конденсаторе, равное разности потенциалов на его обкладках. ,
, (4.13)
(4.13)

 представляет собой среднее значение энергии, приходящейся на единичный объём поля
представляет собой среднее значение энергии, приходящейся на единичный объём поля  .
. (4.14)
(4.14) .
. .
. , r ³ R
, r ³ R



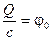 — его потенциал. Тогда:
— его потенциал. Тогда: . (4.15)
. (4.15) . Покажем это.
. Покажем это. то при переносе следующей порции заряда dq придется совершить работу против сил электрического поля
то при переносе следующей порции заряда dq придется совершить работу против сил электрического поля

 . Здесь e — диэлектрическая проницаемость вещества.
. Здесь e — диэлектрическая проницаемость вещества.


