Диэлектрическая проницаемость. Вектор электрического смещения.
В однородное поле плоского конденсатора
Рис. 5.6. Напряженность суммарного поля в диэлектрике:
Здесь мы воспользовались результатом (5.6): s’ = Pn = P и (5.4): Р = e0c Е. Отсюда следует: Е + c Е = Е 0, или:
В последнем выражении e = 1 + c — диэлектрическая проницаемость диэлектрика. Эта величина показывает во сколько раз уменьшается напряжённость электрического поля в среде (Е) по сравнению с вакуумом (Е 0):
Теперь рассмотрим в электрическом поле два контактирующих диэлектрика (рис. 5.7). На границе раздела диэлектриков возникнут связанные заряды противоположные по знаку +
Рис. 5.7. Так меняется напряжённость поля в средах в связи с их поляризацией. Если на границе раздела кроме связанных зарядов присутствуют сторонние заряды с поверхностной плотностью s, то скачок нормальной составляющей напряжённости ещё увеличится:
Перепишем этот результат несколько иначе:
Введём новый вектор, характеризующий поле в диэлектрической среде — вектор электрического смещения
Тогда уравнение (5.9) можно прочесть так:
Если на границе раздела сторонних зарядов нет и s = 0, то:
Это означает, что при переходе через границу раздела диэлектриков нормальная составляющая вектора электрического смещения (и сам вектор!) не меняются. Легко показать, что
Здесь, как и прежде, диэлектрическая проницаемость e = 1 + c. До сих пор мы графически представляли электрическое поле с помощью силовых линий напряжённости. Но в случае полей в неоднородных диэлектриках значительно удобнее пользоваться силовыми линиями вектора смещения. Эти линии не прерываются на границах раздела диэлектриков. В этом и состоит один из главных резонов введения этой характеристики.
|

 введём пластину диэлектрика (рис. 5.6). На гранях этой пластины в результате поляризации возникнут связанные заряды +s’ и –s’. При этом внутри диэлектрика никакие объёмные заряды не появляются. Связанные заряды создадут своё поле
введём пластину диэлектрика (рис. 5.6). На гранях этой пластины в результате поляризации возникнут связанные заряды +s’ и –s’. При этом внутри диэлектрика никакие объёмные заряды не появляются. Связанные заряды создадут своё поле  , направленное навстречу исходному Е 0.
, направленное навстречу исходному Е 0.
 .
. . (5.7)
. (5.7) .
.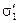 и –
и –  . Связанный заряд границы
. Связанный заряд границы  создаёт в диэлектриках дополнительные поля
создаёт в диэлектриках дополнительные поля  , направленные перпендикулярно границе раздела в противоположные стороны. Выбрав положительное направление нормали к поверхности раздела
, направленные перпендикулярно границе раздела в противоположные стороны. Выбрав положительное направление нормали к поверхности раздела 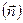 от первого диэлектрика ко второму, запишем изменение нормальной составляющей напряжённости электрического поля при переходе границы между средами:
от первого диэлектрика ко второму, запишем изменение нормальной составляющей напряжённости электрического поля при переходе границы между средами: . (5.8)
. (5.8)
 .
. . (5.9)
. (5.9) :
: . (5.10)
. (5.10) . (5.11)
. (5.11) .
. . Вспомним, что
. Вспомним, что  = e0c
= e0c  . (5.12)
. (5.12)


