В) Ионные диэлектрики
В электрическом поле положительные и отрицательные подрешётки ионной структуры смещаются друг относительно друга, и при этом возникает дипольный момент. Все эти явления, происходящие в диэлектриках в присутствии электрического поля, называются поляризацией. В первом случае это была деформационная поляризация, во втором — ориентационная, в третьем — ионная. Обратимся к количественной мере этих процессов. Для определённости рассмотрим подробнее ориентационную поляризацию полярного диэлектрика. Молекулы такого вещества имеют дипольные моменты. Но в отсутствие электрического поля в однородном диэлектрике нет какого-либо преимущественного направления, и тепловое движение хаотически перемешивает дипольные моменты молекул таким образом, что суммарный момент молекул единицы объёма вещества равен нулю. В электрическом поле на молекулы действуют вращающие моменты, стремящиеся ориентировать диполи вдоль поля. На границах диэлектрика при этом возникают «связанные» заряды с поверхностной плотностью +s’ и –s’ (рис. 5.4.).
Рис. 5.4. Степень поляризации диэлектрика в электрическом поле характеризуется вектором поляризации
Опыт показывает, что вектор поляризации диэлектрика пропорционален напряжённости поля
Здесь: c — диэлектрическая восприимчивость вещества; e0 — знакомая нам электрическая постоянная. В случае неполярного диэлектрика дипольный момент отдельной молекулы, как уже упоминалось, пропорционален напряжённости электрического поля:
Здесь b — поляризуемость молекулы. Тогда суммарный дипольный момент всех молекул в объёме D V будет равен:
Вектор поляризации (поляризованность) в этом случае, как и в случае полярного диэлектрика, оказывается пропорциональным напряжённости поля:
Здесь диэлектрическая восприимчивость c равна произведению числа молекул в единице объёма (n) и коэффициента поляризуемости (b): c = n × b. (5.5) Покажем, что вектор поляризации Рассмотрим однородно поляризованный диэлектрик, выполненный в виде наклонной призмы с основанием S и ребром L, параллельным вектору поляризации
Рис. 5.5. Электрический момент призмы равен q ’ × L = s’ × S × L. Здесь q ’ и s’ — связанный заряд и плотность связанного заряда на основании призмы. Учитывая, что объём призмы равен V = S × L × cosa, этот же электрический момент представим в виде: s’ × SL = P × V = P × SL cosa = Pn × SL. Отсюда легко получить искомое соотношение: s’ = Pn. (5.6) Этот результат позволяет сделать следующие заключения: 1. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации; 2. заряд, прошедший в процессе поляризации через единичную поверхность, нормальную к направлению смещения зарядов, равен модулю вектора поляризации.
|


 , равным векторной сумме дипольных моментов всех молекул единицы объёма вещества (теперь эта сумма не равна нулю):
, равным векторной сумме дипольных моментов всех молекул единицы объёма вещества (теперь эта сумма не равна нулю):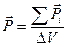 . (5.1)
. (5.1) :
: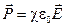 . (5.2)
. (5.2)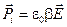 . (5.3)
. (5.3)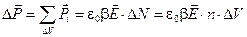 .
.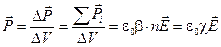 . (5.4)
. (5.4)



