Электродвижущая сила индукции. Закон Фарадея.
В результате многочисленных опытов Фарадею удалось установить, что в замкнутом проводящем контуре возникает индукционный ток и э.д.с. индукции при любом изменении магнитного потока, пронизывающего этот контур. Для того чтобы понять механизм возникновения э.д.с. индукции и уяснить, как же количественно э.д.с. связана с магнитным полем, решим следующую очень непростую задачу (рис. 10.4.). Здесь по двум параллельным горизонтальным проводникам может скользить перемычка ab без трения и без нарушения электрического контакта. Проводники соединены резистором R, поэтому они вместе с перемычкой и резистором образуют замкнутый проводящий контур. Этот контур целиком поместим в однородное магнитное поле
Рис. 10.4. Теперь начнём двигать перемычку с постоянной скоростью За это же время dt поток вектора магнитной индукции сквозь контур изменится на величину:
Отметим, что при заданном направлении нормали Оставив на время наш контур, приглядимся повнимательнее к событиям, развивающимся при движении перемычки внутри этого проводника (рис. 10.5.). Здесь каждый «свободный электрон» движется вместе с перемычкой со скоростью
Рис. 10.5. На заряд, движущийся в магнитном поле, будет действовать сила, параллельная перемычке:
Эта сила не электростатического, а магнитного происхождения, то есть это «сторонняя сила», которую можно задать силовым полем с напряжённостью:
Циркуляция вектора напряжённости
Направление вектора
Результат разделим и умножим на dt, после чего можно сделать следующие шаги:
Здесь мы воспользовались тем, что векторное произведение
Рис. 10.6.
Но этот вектор противоположен нормали, поэтому мы записали, что:
Так мы установили искомую связь э.д.с. индукции и магнитного поля:
Электродвижущая сила индукции равна скорости изменения магнитного потока, пронизывающего замкнутый контур (закон Фарадея). Знак «–» в выражении (10.3) напоминает о правиле Ленца. В нашем примере изменение и скорость изменения потока — положительные величины. Тогда, e < 0. Индукционный ток, I инд. =
Рис. 10.7. Подведём краткий итог. Движение перемычки
Теперь, когда всё так понятно, наведём лёгкую тень сомнения. В нашем контуре работает источник тока, в котором в качестве сторонней силы выступает магнитная сила
Рис.10.8. Легко видеть, что работа этой силы за время dt:
не равна нулю. И в то же время, не далее как на прошлой лекции было неопровержимо показано, что магнитная сила работы не производит (!). Это недоразумение легко разрешается, если принять во внимание, что мы вычислили работу не магнитной силы Лоренца, а только одной её составляющей, направленной вдоль перемычки — Полная магнитная сила:
И вот работа этой полной магнитной силы над электроном за время dt действительно равна нулю:
В этом легко убедиться, подставив в это уравнение F || = eVB и F ^ = eUB. Мы рассмотрели механизм возникновения э.д.с. индукции в частном случае, когда в однородном неизменном магнитном поле меняется площадь контура. Опыт свидетельствует о том, что можно обобщить этот результат: при любом изменении магнитного потока, пронизывающего замкнутый контур, в последнем возникает э.д.с. индукции, численно равная скорости изменения магнитного потока (закон Фарадея).
|

 , перпендикулярное плоскости контура.
, перпендикулярное плоскости контура.
 . За время dt она пройдёт расстояние dl = Vdt, в результате чего площадь контура возрастёт на величину dS = L × Vdt. Здесь L — длина перемычки или расстояние между проводниками.
. За время dt она пройдёт расстояние dl = Vdt, в результате чего площадь контура возрастёт на величину dS = L × Vdt. Здесь L — длина перемычки или расстояние между проводниками. . (10.1)
. (10.1) к плоскости контура, поток и увеличение потока будут положительными. Направление нормали, совпадающее с направлением вектора
к плоскости контура, поток и увеличение потока будут положительными. Направление нормали, совпадающее с направлением вектора 
 . (10.2)
. (10.2) .
. сторонней силы по замкнутому контуру равна э.д.с., действующей в этом контуре (см. лекцию №7):
сторонней силы по замкнутому контуру равна э.д.с., действующей в этом контуре (см. лекцию №7): .
. возьмём от «b» к «a», так как при выбранном направлении нормали
возьмём от «b» к «a», так как при выбранном направлении нормали  .
. .
. — есть вектор изменения поверхности контура
— есть вектор изменения поверхности контура  (рис. 10.6.).
(рис. 10.6.).
 .
. . (10.3)
. (10.3) < 0. Это значит, что он обтекает контур по часовой стрелке (рис. 10.7.). Этот ток создаёт, конечно, своё магнитное поле, которое направлено навстречу исходному полю
< 0. Это значит, что он обтекает контур по часовой стрелке (рис. 10.7.). Этот ток создаёт, конечно, своё магнитное поле, которое направлено навстречу исходному полю 
 приводит к увеличению площади контура (dS), что в свою очередь означает рост потока вектора магнитной индукции через площадь контура (d F = BdS). Всякое изменение магнитного потока приводит к возникновению э.д.с. индукции:
приводит к увеличению площади контура (dS), что в свою очередь означает рост потока вектора магнитной индукции через площадь контура (d F = BdS). Всякое изменение магнитного потока приводит к возникновению э.д.с. индукции: .
. .
.
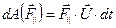
 . Эта составляющая связана со скоростью движения перемычки и электронов в ней со скоростью
. Эта составляющая связана со скоростью движения перемычки и электронов в ней со скоростью  . Но ведь есть и ещё одно движение электронов: вдоль перемычки со скоростью направленного движения
. Но ведь есть и ещё одно движение электронов: вдоль перемычки со скоростью направленного движения  =
=  . (Рис. 10.8. Воспользуйтесь правилом левой руки. Учитывайте при этом, что рассматривается движение электрона.)
. (Рис. 10.8. Воспользуйтесь правилом левой руки. Учитывайте при этом, что рассматривается движение электрона.) .
. .
.


