Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля.
Посмотрим, как влияет э.д.с. самоиндукции на процесс установления тока в цепи, содержащей индуктивность. В цепи, представленной на схеме 10.10, течёт ток. Отключим источник e, разомкнув в момент времени t = 0 ключ К. Ток в катушке начинает убывать, но при этом возникает э.д.с. самоиндукции, поддерживающая убывающий ток.
Рис. 10.10. Запишем для новой схемы 10.10. b уравнение правила напряжений Кирхгофа:
Разделяем переменные и интегрируем:
Пропотенцировав последнее уравнение, получим:
Постоянную интегрирования найдём, воспользовавшись начальным условием: в момент отключения источника t = 0, ток в катушке I (0) = I 0. Отсюда следует, что c = I 0 и поэтому закон изменения тока в цепи приобретает вид:
График этой зависимости приведён на рис. 10.11. Оказывается, ток в цепи, после выключения источника, будет убывать по экспоненциальному закону и станет равным нулю только спустя t = ¥.
Рис. 10.11. Вы и сами теперь легко покажете, что при включении источника (после замыкания ключа К) ток будет нарастать тоже по экспоненциальному закону, асимптотически приближаясь к значению I 0 (см. рис. 10.11.).
Но вернёмся к первоначальной задаче размыкания цепи. Мы отключили в цепи источник питания (разомкнули ключ К), но ток — теперь в цепи 10.8. b — продолжает течь. Где черпается энергия, обеспечивающая бесконечное течение этого убывающего тока? Ток поддерживается электродвижущей силой самоиндукции e = dA = eСИ× I × dt = – LIdI. Ток будет убывать от начального значения I 0 до нуля. Проинтегрировав последнее выражение в этих пределах, получим полную работу убывающего тока:
Совершение этой работы сопровождается двумя процессами: исчезновением тока в цепи и исчезновением магнитного поля катушки индуктивности. С чем же связана была выделившаяся энергия? Где она была локализована? Располагалась ли она в проводниках и связана ли она с направленным движением носителей заряда? Или она локализована в объёме соленоида, в его магнитном поле? Опыт даёт ответ на эти вопросы: энергия электрического тока связана с его магнитным полем и распределена в пространстве, занятом этим полем. Несколько изменим выражение (10.9), учтя, что для длинного соленоида справедливы следующие утверждения: L = m0 n 2 Sl (10.5) — индуктивность; B 0 = m0 nI 0 (9.17) — поле соленоида. Эти выражения используем в (10.9) и получим новое уравнение для полной работы экстратока размыкания, или — начального запаса энергии магнитного поля:
Здесь V = S × l — объём соленоида (магнитного поля!). Энергия катушки с током пропорциональна квадрату вектора магнитной индукции. Разделив эту энергию на объём магнитного поля, получим среднюю плотность энергии:
Это выражение очень похоже на выражение плотности энергии электростатического поля:
Обратите внимание: в сходных уравнениях, если e0 — в числителе, m0 — непременно в знаменателе. Зная плотность энергии в каждой точке магнитного поля, мы теперь легко найдём энергию, сосредоточенную в любом объёме V поля. Локальная плотность энергии в заданной точке поля:
Значит, dW = w dV и энергия в объёме V равна:
Лекция 11 «Электрические колебания» План лекции 1. Колебательные контуры. Квазистационарные токи. 2. Собственные электрические колебания. 2.1. Собственные незатухающие колебания. 2.2. Собственные затухающие колебания. 3. Вынужденные электрические колебания. 3.1. Сопротивление в цепи переменного тока. 3.2. Ёмкость в цепи переменного тока. 3.3. Индуктивность в цепи переменного тока. 3.4. Вынужденные колебания. Резонанс. 3.5. Проблема косинуса фи.
|


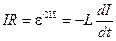 .
.

 .
. . (10.7)
. (10.7)
 . (10.8)
. (10.8) . За время dt убывающий ток совершит работу:
. За время dt убывающий ток совершит работу: . (10.9)
. (10.9) . (10.10)
. (10.10) [
[  ]. (10.11)
]. (10.11)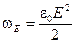 .
.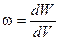 .
. .
.


