Собственные затухающие колебания
Собственные затухающие колебания происходят в колебательном контуре RLC (рис. 11.1. и 11.5.).
Рис. 11.5. Эти колебания можно описать следующим дифференциальным уравнением (правило напряжений Кирхгофа): IR – U C = eСИ. (11.6) Здесь по-прежнему: I = Учитывая эти соотношения, уравнению (11.6) придадим следующий вид:
Здесь d = Уравнение (11.7) — дифференциальное уравнение собственных затухающих электрических колебаний. Если в системе q = Ae –dtcos(w t + j). (11.8) Здесь А и j — постоянные, которые можно найти, воспользовавшись начальными условиями, а частота колебаний:
Убедиться в том, что функция (11.8) действительно является решением дифференциального уравнения (11.7), каждый может самостоятельно, подставив (11.8) в (11.7). Важной характеристикой затухающего процесса является логарифмический декремент затухания — логарифм отношения амплитуд двух соседних колебаний (рис. 11.2 б):
Логарифмический декремент затухания равен произведению коэффициента затухания d на время одного полного колебания (период) Т. Процесс затухания колебания до нуля продолжается бесконечное время, поэтому условно принято считать, что процесс затух, если амплитуда колебаний уменьшилась в е раз. Вычислим, сколько же колебаний Ne произойдёт, пока амплитуда уменьшится в е раз?
Отсюда следует, что d NeT = Ne × d = 1. Или:
Логарифмический декремент затухания d обратен числу колебаний, по истечению которых амплитуда падает в е раз. В радиотехнике для энергетической характеристики затухания часто используют величину, которая получила название добротность контура:
Покажем, что добротность с точностью до 2p равна отношению энергии Е, запасенной в контуре, к убыли энергии за один период (–D Е):
Энергия, запасенная в контуре, пропорциональна квадрату амплитуды заряда конденсатора:
Относительная убыль энергии за период равна:
При малом затухании (когда d << 1) можно приблизительно принять, что: e –2 d = 1 – 2 d. Тогда относительная убыль энергии:
или
Мы рассмотрели затухающие колебания при малом затухании, когда Если затухание столь значительно, что d2 ³
Величина критического сопротивления зависит только от величины индуктивности и ёмкости колебательного контура.
|

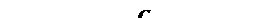
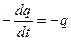 ; U C =
; U C =  ; eСИ =
; eСИ =  =
=  =
=  .
. ;
;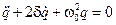 . (11.7)
. (11.7) — коэффициент затухания;
— коэффициент затухания;  =
=  — частота собственных незатухающих колебаний.
— частота собственных незатухающих колебаний. , то решением этого уравнения является следующая функция:
, то решением этого уравнения является следующая функция: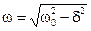 . (11.9)
. (11.9) . (11.10)
. (11.10)
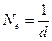 и
и  .
. . (11.11)
. (11.11) .
. .
.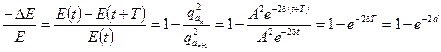 .
. ,
, ;
;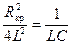 ;
; . (11.13)
. (11.13)


