Решения систем линейных уравнений методом Гаусса
Следовательно, система имеет единственное решение. Найдем решение системы:
Следовательно, система имеет бесконечное множество решений, каждое из которых может быть найдено по формулам:
,
Пример 3
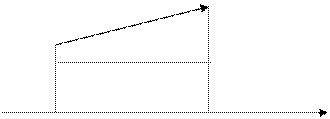
Следовательно, система несовместна. Векторная алгебра Основные понятия Вектором будем называть направленный отрезок
Векторы, параллельные одной прямой или лежащие на этой прямой, называются коллинеарными. Два вектора Векторы Произведением вектора Проекцией вектора
 
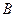
0
Проекция вектора на ось равна длине вектора, умноженной на косинус угла между положительным направлением оси и вектором, пр l Если заданы точки
Теперь найдем разложение вектора Векторы
ij У Х Рис. 2 Выражение вида
|
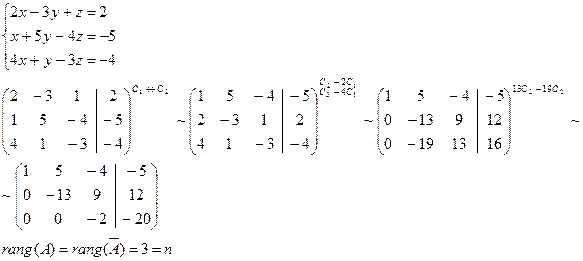Пример 1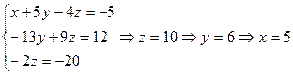
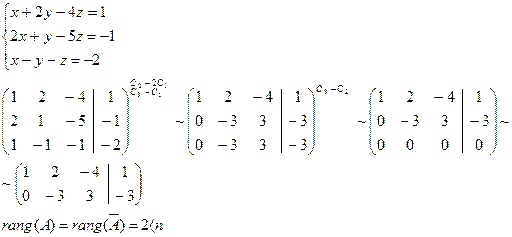
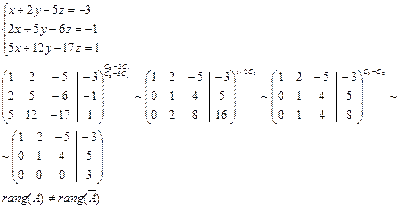
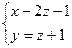
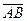, в котором 
- начало, а 
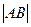- длина вектора.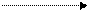
и 
называются равными, если они имеют одно и то же направление, и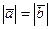 
.
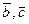называются компланарными, если они лежат в одной плоскости или параллельных плоскостях.
называется вектор, длина которого равна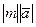 
, коллинеарный вектору 
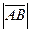на ось 
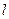называется разность 
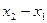между координатами проекций конца и начала вектора 
.
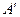
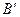
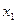
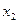
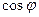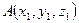и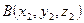 
, то тогда вектор
.
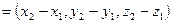на составляющие, направленные по осям координат,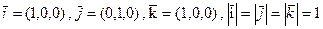
образуют базис в пространстве R3 и называются ортами (рис 2).
Z
k 
называется разложением вектора 
