Векторное произведение двух векторов
Векторным произведением двух векторов а) б) перпендикулярен плоскости, образованной векторами
Замечание. Длина вектора Свойства векторного произведения 1. Векторное произведение равно нулю, если хотя бы один из векторов нулевой или векторы 2. 3. Векторное произведение ортов Исходя из определения векторного произведения, получим следующие равенства: Z
 (рис. 5). X 
Векторное произведение двух векторов, заданных своими координатами Пусть даны векторы Тогда их векторное произведение вычисляется по формуле
1. Найти векторное произведение двух векторов
2. Найти площадь треугольника Найдем векторы
3. Пусть даны векторы Найти длину их векторного произведения
4. Упростить выражение
5. Доказать тождество
Cмешанное произведение трех векторов Определение. Смешанным произведением трех векторов Пусть даны три вектора
|
и 
называется вектор 
такой, что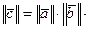
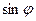, где 
- угол между векторами;
, можно наблюдать перемещение вектора 
.
.
, 
, 
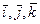
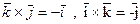Y
и 
.
.
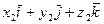, заданного координатами своих вершин, 
и 
. 
.
. 
.
и 
, известно, что 
и угол между векторами 
и 
равен 
.
.
.
= 
=
= 
= 
= 
+ 
.
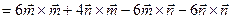
называется выражение вида 
.
, 
, 
, тогда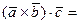
= 
.
