Операции над матрицами
Отметьте правильный ответ Из неравенства Коши-Буняковского для унитарного пространства С2[a,b] непрерывных на отрезке [a,b] функций вещественно переменными с комплексным значениям следует, что: £
£
R
£
Решение систем уравнений методом Крамера 1. Определитель системы Вспомогательные определители
Решение системы
2. Определитель системы вычислим по формуле (4)
Вспомогательный определитель
определитель
определитель
Пусть дана линейная система
Таблица из числа Если Диагональ этой матрицы, составленная из элементов Квадратная матрица порядка Пусть дана матрица, А = Операции над матрицами Суммой А + В двух матриц А = ( Произведением kА матрицы А = ( В = ( Произведением матрицы А = ( Пусть дана квадратная матрица А = Если определитель квадратной матрицы равен нулю, то матрица называется вырожденной (особенной), и невырожденной (неособенной) – в противоположном случае. Матрица В называется обратной для матрицы А, если АВ = ВА = Е и будем ее обозначать В = А-1. Для невырожденной матрицы А существует обратная матрица, причем единственная и А-1 = Примеры 1. 2. 3. Дана матрица
|






 .
. ,
,  .
.
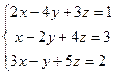
 = 2(-2)5+1(-1)3+3(-4)4 – (3(-2)3+2(-1)4+5(-4)1) =-25
= 2(-2)5+1(-1)3+3(-4)4 – (3(-2)3+2(-1)4+5(-4)1) =-25 вычислим разложением по элементам первой строки
вычислим разложением по элементам первой строки =
=  ,
, вычислим разложением по элементам первого столбца
вычислим разложением по элементам первого столбца ,
, вычислим разложением по элементам третьей строки
вычислим разложением по элементам третьей строки
 .
.
 .
. элементов
элементов  называется матрицей из
называется матрицей из  строк и
строк и 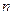 столбцов;
столбцов; называются элементами матрицы.
называются элементами матрицы. , то матрица называется квадратной порядка
, то матрица называется квадратной порядка  , называется главной диагональю.
, называется главной диагональю.
 называется транспонированной матрицей матрицы А.
называется транспонированной матрицей матрицы А. ) размерности
) размерности  ) такая, что
) такая, что  .
. k
k  ) размерности
) размерности  называется матрица С = АВ = (
называется матрица С = АВ = ( ) размерности
) размерности  такая, что
такая, что 
 .
. и ее определитель
и ее определитель  А
А 
 .
. .
. .
.

 =
=  , найти обратную.
, найти обратную.


 ,
, ,
,  ,
,  =
=  ,
, ,
,  ,
,  .
. .
.


