Скалярное произведение двух векторов
Скалярное произведение векторов
Пусть даны два вектора Скалярное произведение двух векторов в этом случае вычисляется по формуле
Используя скалярное произведение, запишем формулы для вычисления проекции вектора
Нормой вектора Если вектор
Направляющие косинусы вектора Из определения скалярного произведения двух векторов имеем Пусть дан вектор
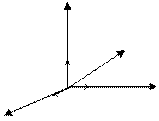 Z Z
X
Тогда Пусть даны два вектора Вычислить 1. Скалярное произведение
2. Угол между векторами
3. Проекции векторов друг на друга
4. Направляющие косинусы вектора
5. Определить, при каком значении
6. Найти вектор Из условия коллинеарности 7. Даны векторы Вычислить скалярное произведение векторов
8. Найти норму вектора
|

 и
и  определяется соотношением
определяется соотношением , где
, где  - угол между векторами
- угол между векторами  .
.
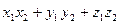 .
. на вектор
на вектор  и наоборот,
и наоборот, ,
, 
 ,
, 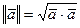 .
. задан в декартовой системе координат, то его длина
задан в декартовой системе координат, то его длина равна норме вектора.
равна норме вектора. , где
, где 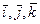 .
.


 Y
Y , где
, где 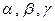 - углы, образованные вектором
- углы, образованные вектором  .
.

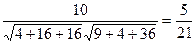 ,
,  .
. ,
, 

 векторы
векторы  будут ортогональны.
будут ортогональны.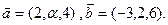
 , отсюда
, отсюда  .
. , коллинеарный вектору
, коллинеарный вектору 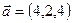 и удовлетворяющий условию
и удовлетворяющий условию 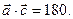
 , тогда
, тогда  , отсюда
, отсюда 
 и
и  , известно, что
, известно, что  и угол между векторами
и угол между векторами  и
и  равен
равен  .
.

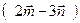
 =
= 


 .
. .
.


