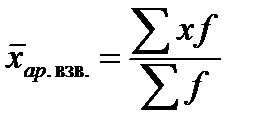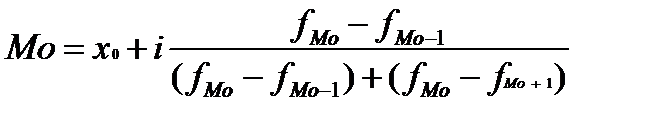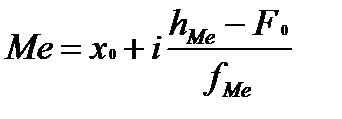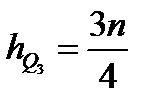Показатели распределения единиц совокупности.

Средняя арифметическая для дискретного ряда распределения исчисляется по формуле средней арифметической взвешенной:

где x - варианты значений признака, f - частота повторения данного варианта.

Для интервальных рядов распределения в качестве вариантов значений признака используют значение середины соответствующего интервала.

Мода (Мо) - наиболее часто встречающееся значение признака. В дискретном ряду - это варианта с наибольшей частотой. В интервальном ряду сначала определяется модальный интервал, т. е. тот интервал, который имеет наибольшую частоту (повторяемость). При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака х.

Конкретное значение моды определяется по формуле:

где х_о - нижняя граница модального интервала, i - величина интервала, f_Мо - частота модального интервала, f_Мо-1 - частота интервала, предшествующего модальному, f_Мо+1 - частота интервала, следующего за модальным.

Медиана (Me) соответствует варианте, стоящей в середине ранжированного ряда. Медиана – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака больше медианного уровня, а у другой – меньше его. При этом основное свойство медианы заключается в том, что сумма абсолютных значений признака от медианы меньше, чем от любой другой величины:

Положение медианы определяется ее номером:

где n - число единиц в совокупности (если n – нечетное число, то в числителе n+1).

По накопленным частотам определяют ее численное значение в дискретном вариационном ряду.

В интервальном ряду распределения медиану определяют с помощью формулы. При этом сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений (h_Ме).

Численное значение медианы определяется по формуле:

где х₀ - нижняя граница медианного интервала, i - величина интервала, h_Ме – порядковый номер медианы, F_о - накопленная частота интервала, предшествующего медианному, f_Ме - частота медианного интервала.

Моду и медиану можно определить на основе графического изображения ряда. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной.

Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Расчёт таких показателей, как кватрили и децили производится по алгоритму расчёта медианы. При этом надо учитывать, что первый квартиль (Q₁) – значение признака у последней единицы первой четверти единиц совокупности, второй квартиль (Q₂) соответствует значению медианы, третий квартиль (Q₃) – значение признака у единицы, делящей ранжированный ряд на ¾ и ¼.

Децили – значения признака у единицы, находящейся между первым и вторым десятком единиц совокупности (первый дециль D₁), вторым и третьим (второй дециль D₂), третьим и четвертым десятком (третий дециль D₃) и т.д.

При расчёте квартилей и децилей сначала находим порядковые номера. Например, порядковый номер первого квартиля:

третьего квариля:

где n - число единиц в совокупности (если n – нечетное число, то в числителе n+1).

Порядковый номер первого дециля:

Порядковый номер второго дециля:

При дискретном вариационном ряде значение децилей определяем по значению, соответствующему порядковому номеру. Если ряд интервальный, значение рассчитываем аналогично формуле медианы, учитывая порядковый номер квартиля или дециля.

При изучении распределения показателей для характеристики их дифференциации у отдельных групп совокупности использую отношение девятого дециля (D₉) и первого (D₁) – децильный коэффициент дифференциации (ДКД):