А) размах вариации
где хmax и xmin соответственно значения наибольшей и наименьшей варианты признака в данной совокупности. б) среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений отдельных вариантов xi от их средней х:
в) дисперсия - средняя арифметическая из квадратов отклонений отдельных вариантов от среднего значения признака:
В отличие от математики, статистика оперирует не абстрактными, а смысловыми величинами, имеющими размерность. Поэтому и дисперсия здесь не безразмерная, как в математике, а сопровождается квадратической размерностью. Например, если статистическая величина измеряется в годах, или рублях, то дисперсия отклонений получится в «квадратных» годах или в «квадратных» рублях. Для получения обычной размерности находится среднее квадратическое отклонение (σ). г) среднее квадратическое отклонение - корень квадратный из дисперсии
Однако значения средних отклонений, как любой абсолютной величины, служат лишь количественной мерой анализа статистической совокупности. Для качественного анализа применяются относительные критерии, называемые коэффициентами вариации. Рассмотрим основные относительные величины, используемые при анализе вариации: Линейный коэффициент вариации - отношение среднего линейного отклонения к средней величине:
Квадратический коэффициент вариации - отношение среднего квадратического отклонения к средней величине:
С помощью линейного коэффициента вариации принципиальный вывод о типичности или нетипичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии. Если он не превышает 33 %, то совокупность по рассматриваемому признаку можно считать однородной. Коэффициент осцилляции – отношение размаха вариации к средней величине
3. Изучение степени неравномерности распределения суммарного показателя. Степень неравномерности распределения определенного суммарного показателя между отдельными группами вариационного ряда наглядно показывают кривая Лоренца и рассчитанный на её основе коэффициент Джини. Кривая Лоренцаиспользуется для изображения уровня концентрации явления. Для ее построения на обе оси координат наносят процентную масштабную шкалу (от 0 до 100 %). При этом распределение единиц совокупности и распределение суммарного показателя должны быть представлены в относительных показателях, и для обоих распределений рассчитываются накопленные (кумулятивные) итоги. Для точек кривой абсциссами служат кумулятивные итоги единиц совокупности (например, доля городов в общем их количестве с численностью населения до определенного значения), а ординатами — значения признака (например, кумулятивный итог численности городского населения). Равномерное распределение признака будет представлено в таком случае диагональю, называемой «линией равномерного распределения», а неравномерное — «линией Лоренца», отклонение которой от диагонали и характеризует степень неравномерности. Чем больше фактическое распределение двух показателей отклоняется от равномерного, тем больше кривая Лоренца удалена от диагонали. Несколько кривых Лоренца, построенных на одном квадрате, используют для сравнения уровня концентрации изучаемого показателя во времени и в пространстве (по разным территориям). При количественной оценке степени концентрации часто используют коэффициент Джини (G):
где wi– доля единиц совокупности (частость), qiи qi+1– доля суммарного показателя i-ой и последующей группы. Чем ближе значение коэффициента Джини к единице, тем больше степень концентрации изучаемого суммарного показателя в отдельных группах единиц совокупности (степень неравномерности распределения).
|

 ,
, (простая)
(простая) (взвешенная)
(взвешенная) (простая)
(простая) (взвешенная)
(взвешенная)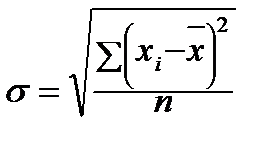 (простая)
(простая) (взвешенная)
(взвешенная)


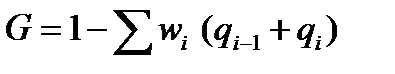 ,
,


