Дифференциальные уравнения равновесия жидкости
Допустим, мы имеем произвольные массовые силы. Обозначим единичные массовые силы по соотв.направлениям след.образом:X,Y,Z. Запишем уравнения Эйлера: Домножим ур-ния на dx,dy,dz и сложим их: Xdx+Ydy+Zdz-1/ρ( Выражение, стоящее в скобках представляет собой полный дифференциал давления: dp=ρ(Xdx+Ydy+Zdz). Данное выражение определяет приращение давления при приращении координат dx,dy,dz. Рассм.частный случай,когда действует только сила тяжести: Y=X=0; Z=-g; dp=-ρgdz. Проинтегрируем обе части:p=-ρgz+c. Константу с находим по координате свободной пов-ти: p0==-ρgz0+c; c=p0+ρgz0; p+ρgz= p0+ρgz0;/ разделим на ρg z+p/ρg=z0+p0/ρg. Таким образом з-н Паскаля явл-ся частным случаем ДУ равновесия жидкостей.
Пьезометрическая высота. Вакуум.
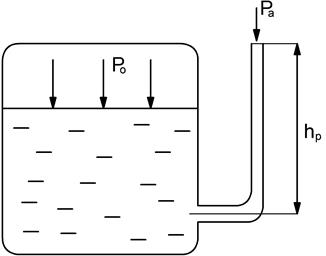
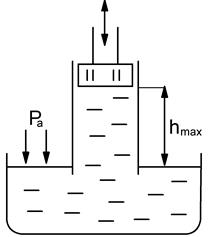
Пьезометрическую высоту измеряют по пьезометру. Зачастую давление выражается через соответствующую высоту. Если абсолютное давление в жидкости или газе ниже атмосферного, то говорят, что имеет разрежение или вакуум. Вакуум измеряется недостатком до атмосферного давления.
Максимальная высота, на которую может подняться жидкость с помощью вакуума:
Кинематика и динамика жидкости. Основные понятия. Кинематика жидкости отличается от кинематики твердого тела поскольку в твердом теле частицы жестко связаны друг с другом, а в жидкости они движутся друг относительно друга. Задача кинематики: определение скорости в любой точке жидкой среды. Рассмотрим вначале идеальную жидкость, т.е. жидкость в кот. будет отсутствовать вязкость. Движение жидкости может быть установившемся и не установившемся. Установившемся называют течение жидкости неизменное во времени при котором скорость жидкости и давление являются только функциями координат и не зависят от времени.
Неустановившемся называется течение параметры которого скорость и давление изменяются в заданной точке рассматриваемого пространства.
Линия тока – кривая, в каждой точке которой вектор скорости направлен по касательной к ней.
Часть потока, заключенная в трубке тока наз. элементарной струйкой тока. Если диаметр трубки тока стянуть к нулю, то получим линию тока. Будем абстрактно считать, что трубка тока явл. непроницаемой поверхностью, т. е. ни одна частица не может ни попасть внутрь трубки, ни покинуть её. Будем считать большие потоки как совокупность элементарных струек, кот. скользят друг по другу, но не перемешиваются. Живое сечение – это поверхность, в пределах потока, проведенная нормально к линиям тока. Течения бывают напорными и безнапорными. Расход – это количество жидкости, протекающее через живое сечение потока в единицу времени.
|

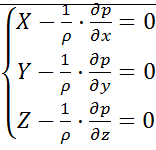
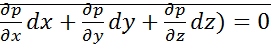 .
.
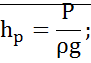
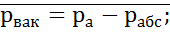
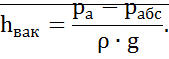
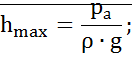
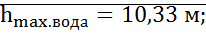
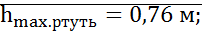
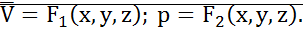
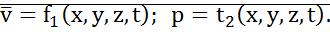
 Если замкнутым контуром пересечь движущуюся жидкость и через все ее точки провести линии тока, то получится трубчатая поверхность, которую называют – трубка тока.
Если замкнутым контуром пересечь движущуюся жидкость и через все ее точки провести линии тока, то получится трубчатая поверхность, которую называют – трубка тока.


