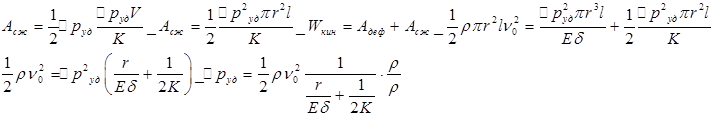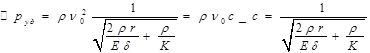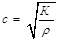Прямой гидравлический удар.
Гидравлическим ударом называется явление резкого повышения давления в напорном трубопроводе при внезапном торможении потока движущейся жидкости. Гидроудар – колебательный процесс, возникающий в упругом трубопроводе с капельной жидкостью. Этот процесс чрезвычайно быстротечный и характеризующийся чередованием резких повышений и понижений давления, связанных с упругой деформацией жидкости и стенок русла. Впервые это явление было рассмотрено в 1808г. Жуковским Н.Е.
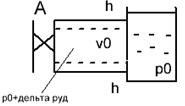
Пусть в конце трубы, по которой течет жидкость со скоростью υ0, произведем мгновенное закрытие задвижки А. Кинетическая энергия жидкости преобразуется в энергию деформации стенок трубы и повышения давления жидкости. Сечение n-n будет перемещаться вправо (рис.а) со скоростью с, называемой скоростью ударной волны. Ударной волной является область, в которой давление равно p0+∆руд. При достижении сечений n-n резервуара (рис.б) скорость течения жидкости становится равным 0, а давление в трубе становится равным p0+∆руд. Под действием перепада давления ∆руд жидкость устремляется в резервуар (рис.в). Сечение n-n начинается перемещаться влево со скоростью с, энергия деформации преобразуется в кинетическую энергию жидкости. Когда сечение n-n достигнет задвижки А (рис.г) равновесное состояние не наступит, поскольку жидкость приобрела кинетическую энергию. Под действием этой энергии жидкость продолжает из трубы перетекать в резервуар. В результате чего в трубе возрастает область пониженного давления po’-∆руд сечение n-n перемещается вправо со скоростью с (рис.д). При достижении сечением n-n резервуара вся труба оказывается сжатой (давление p0-∆руд). Под действием перепада давления ∆руд жидкость начинает из резервуара течь в трубу (рис.ж), при этом сечение n-n перемещается влево со скоростью с. При достижении сечением задвижки А (рис.з) деформация в трубе исчезает, но под действием скорости v0 жидкость снова начинает деформировать трубу в сторону расширения (переходим к рис.а). Процесс повторяется. В ходе эксперимента Жуковский наблюдал до 12 полных колебаний ч постепенным уменьшением ∆руд. Связано это с потерями на трение и рассеивание энергии в резервуаре.
Работа деформации стенок трубки представляет собой работу сил давления на пути ∆r.
Правую часть умножим и разделим на ρ
Если стенки трубки будут абсолютно жесткими, то модуль упругости стремится к бесконечности, Это есть скорость звука в однородной среде с пластичностью ρ и модулем упругости К. С=1435м/с – вода с=(1200..1400)м/с
|

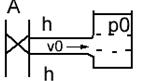
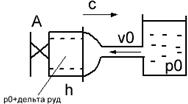 а) г)
а) г)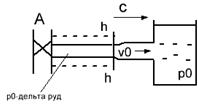
 б) д)
б) д)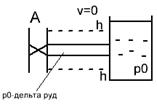
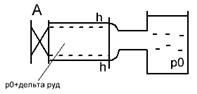 в) ж)
в) ж)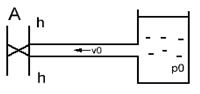
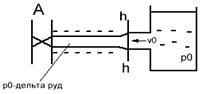 з) е)
з) е)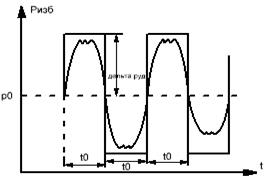 Подобная картина будет наблюдаться в том случае, если данная картина будет иметь давление р>∆руд. Если приведенное неравенство не выполняется, то переходный процесс будет происходить несколько по- иному. Первоначальный скачок давления будет таким же как и в предыдущем случае, после чего давление крана А падает практически до нуля. В результате возникает кавитация, амплитуда колебаний снижается, частота увеличивается. Начальное превышение давления при гидроударе может быть определено по следующей формуле
Подобная картина будет наблюдаться в том случае, если данная картина будет иметь давление р>∆руд. Если приведенное неравенство не выполняется, то переходный процесс будет происходить несколько по- иному. Первоначальный скачок давления будет таким же как и в предыдущем случае, после чего давление крана А падает практически до нуля. В результате возникает кавитация, амплитуда колебаний снижается, частота увеличивается. Начальное превышение давления при гидроударе может быть определено по следующей формуле 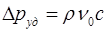 , где
, где 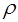 - плотность жидкости, v0 – начальная скорость течения жидкости, с – скорость ударной волны. Неизвестная в формуле является величина с. Определим ударные превышения давления, приняв допущения, что кинетическая энергия жидкости преобразуется в энергию деформации стенок трубки и работу сжатия жидкости.
- плотность жидкости, v0 – начальная скорость течения жидкости, с – скорость ударной волны. Неизвестная в формуле является величина с. Определим ударные превышения давления, приняв допущения, что кинетическая энергия жидкости преобразуется в энергию деформации стенок трубки и работу сжатия жидкости.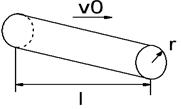 Кинетическая энергия цилиндрического объема жидкости может быть определена
Кинетическая энергия цилиндрического объема жидкости может быть определена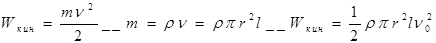
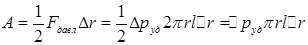 По закону Гука механическое напряжение σ=
По закону Гука механическое напряжение σ= 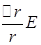 , E-модуль упругости материала трубки. С другой стороны
, E-модуль упругости материала трубки. С другой стороны 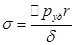 ,δ- толщина стенки
,δ- толщина стенки 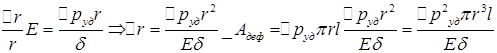
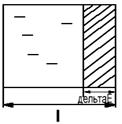 Работа сжатия жидкости представляет собой работу сил давления на пути
Работа сжатия жидкости представляет собой работу сил давления на пути 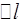
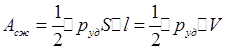 По закону Гука для жидкостей
По закону Гука для жидкостей 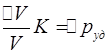 ,где к – обычный модуль упругости жидкости Выразив из з-на Гука дельта V, подставим
,где к – обычный модуль упругости жидкости Выразив из з-на Гука дельта V, подставим