Динамика одномассовой и двухмассовой систем
1) Динамика идеальной одномассовой системы
Переходный процесс будет описываться выражением:
Свободное движение вращающейся массы J описывается следующими диф.уравнениями: N(p)= a После решения диф. уравнения получаем выражение для свободной составляющей переходного процесса: 3)Динамика демпфированной двухмассовой системы. В реальности существуют некоторые диссипативные силы, которые способствуют влиянию гашения механических колебаний При наличии демпфирующего устройства возникает сила трения 1-го рода Дифференциальные уравнения, описывающие данную систему имеют вид:
Разделим обе части уравнения на массу
Собственная составляющая выходной величины будет изменяться по закону
|

 Механическая часть каждого привода в общем случае является многомассовой системой со многими сложными кинематическими связями. Кроме того, существует влияние одних приводов на другие, поэтому оценка динамики ПРМ может быть осуществлена с помощью средств вычислительной техники. На практике зачастую для упрощения пренебрегают связями между отдельными звеньями, а каждый конкретный привод рассматривается как одно-или много массовая система
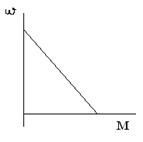
Механическая часть каждого привода в общем случае является многомассовой системой со многими сложными кинематическими связями. Кроме того, существует влияние одних приводов на другие, поэтому оценка динамики ПРМ может быть осуществлена с помощью средств вычислительной техники. На практике зачастую для упрощения пренебрегают связями между отдельными звеньями, а каждый конкретный привод рассматривается как одно-или много массовая система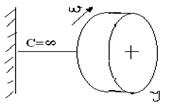 В случае линейной характиристики двигателя
В случае линейной характиристики двигателя 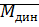 =a+b
=a+b 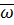
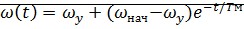 , где Tм=J/β
, где Tм=J/β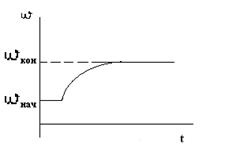 Динамика недемпфированной двухмассовой системы
Динамика недемпфированной двухмассовой системы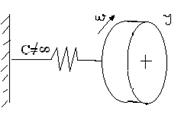 В такой системе возникает момент упругости:
В такой системе возникает момент упругости: 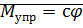
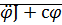 =0
=0 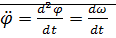 Если приведем уравнения к операторному виду, характеристический полином будет иметь вид:
Если приведем уравнения к операторному виду, характеристический полином будет иметь вид: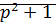 a
a 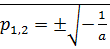 =
= 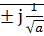
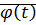 =
= 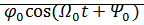
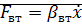
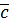 – коэф. вязкого трения
– коэф. вязкого трения 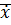 - скорость движенния
- скорость движенния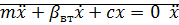 =
= 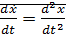
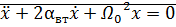 , где
, где 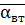 – коэф. затухания
– коэф. затухания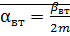
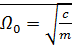 – собственная круговая частота системы
– собственная круговая частота системы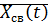 =
= 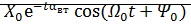
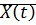 =
= 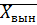 +
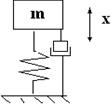
+ 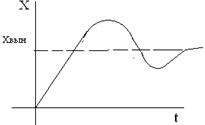 Явление затухания колебаний под действием вязкого трения используется в приводах ПРМ. Для этого применяются так называемые демпферы. Как правило, демпфер это гидро или пневмо цилиндр с перепускными каналами регулируемого сечения
Явление затухания колебаний под действием вязкого трения используется в приводах ПРМ. Для этого применяются так называемые демпферы. Как правило, демпфер это гидро или пневмо цилиндр с перепускными каналами регулируемого сечения


