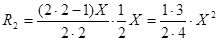Вывод рекуррентной формулы для вычисления члена ряда

Различают большой круг биотического обмена (биосферный) и малый (биогеоценотический).

 

Вычисление суммы бесконечного ряда с заданной точностью

Пусть задана последовательность чисел R₁, R₂, R₃,…,R_n,…. Выражение
R₁ + R₂ + R₃ +…+ R_n +… называют бесконечным рядом, или просто рядом, а числа R₁, R₂, R₃,… - членами ряда. При этом имеют в виду, что накопление суммы ряда начинается с первых его членов. Сумма S_n = называется частичной суммой ряда: при n=1 – первой частичной суммой, при n=2 – второй частичной суммой и так далее.

Называется ряд сходящимся, если последовательность его частичныхсумм имеет предел, и расходящимся – в противном случае. Понятие суммы ряда можно расширить [9], и тогда некоторые расходящиеся ряды также будут обладать суммами. Именно расширенное понимание суммы ряда будет использовано при разработке алгоритмов при следующей постановке задачи: накопление суммы следует выполнять до тех пор, пока очередной член ряда по абсолютной величине больше заданной величины ε.

В общем случае все или часть членов ряда могут быть заданы выражениями, зависящими от номера члена ряда и переменных. Например,

Тогда возникает вопрос, как минимизировать объём вычислений - вычислять значение очередного члена ряда по общей формуле члена ряда (в приведённом примере её представляет выражение под знаком суммы), по рекуррентной формуле (её вывод представлен ниже) или использовать рекуррентные формулы лишь для частей выражения члена ряда (см. ниже).

Вывод рекуррентной формулы для вычисления члена ряда

Пусть требуется найти ряд чисел R₁, R₂, R₃,…, последовательно вычисляя их по формулам

, , …,

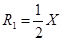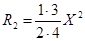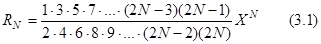
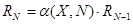Для сокращения вычислений в данном случае удобно воспользоваться рекуррентной формулой вида , позволяющей вычислить значение R_N при N>1, зная значение предыдущего члена ряда R_N-1, где 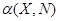- выражение, которое можно получить после упрощения отношения выражения в формуле (3.1) для N к выражению для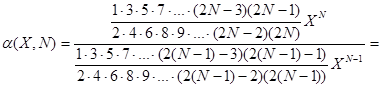
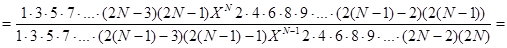
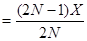
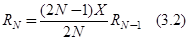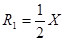N-1:

 

Таким образом, рекуррентная формула примет вид .

Из сравнения общей формулы члена ряда (3.1) и рекуррентной (3.2) видно, что рекуррентная формула значительно упрощает вычисления. Применим ее для N=2, 3 и 4 зная, что :