ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
Рассмотрим упрощенную схему компенсации реактивной мощности.
Математическая модель технологического процесса компенсации реактивной мощности – это математическое выражение, объясняющее изменение напряжения питания сети от величины реактивной мощности.
где
Ограничением при поиске оптимального варианта являются границы допустимого диапазона по напряжению. В случае, когда напряжение вне допустимого диапазона, поиск оптимального варианта необходимо производить только среди тех компенсаторов, чувствительность которых по напряжению U является достаточной для вхождения в допустимую область. Если это условие нельзя постичь, то надо выбрать то компенсирующее устройство, для которого произведение наибольшее и, таким образом, приближение напряжения к одной из границ допустимого диапазона изменения напряжения будет максимальным при минимальном увеличении активных потерь в сети. На базе изложенного можно предложить следующий план переключений реактивных мощностей: 1. Если напряжение Uk остается в допустимом диапазоне: а) нужно включить последовательно компенсирующие мощности для которых:
б) нужно выключить последовательно компенсирующие мощности, для которых:
2. Если напряжение Uk находится вне допустимого диапазона нужно выбрать то компенсирующее устройство для которого:
при этом знак U нужно выбрать адекватно направлению движения к допустимой области. На базе полученных аналитических выражений можно сделать следующие выводы: 1) В однородных сетях выбор оптимального варианта можно делать только по значению f2, т.е. только по постоянным потерям ∆P2, так как f1=0. Пока напряжение остается в допустимом диапазоне, в начале нужно выключать компенсирующие устройства с наибольшими собственными термическими потерями и расходами на охлаждение независимо от знака U. Действительно, в однородных сетях естественное потокораспределение предопределяет минимальные потери и компенсация в этом смысле здесь не эффективна. 2) В оптимальном варианте непосредственно 3) Переключение компенсирующих мощностей, поскольку оно изменяет топологию сети и влияет на определение чувствительности других источников, может привести к переупорядочиванию вариантов с точки зрения их эффективности. Следовательно, при многошаговой процедуре оптимизации нужно пересматривать после каждого шага устраненные варианты на предыдущих этапах. Предложенная простая математическая модель позволяет легко определить две важные характеристики источников реактивной мощности – чувствительность напряжения и потерь активной мощности в сети при изменении узловой реактивной мощности.
|

 Рисунок 6 Упрощенная схема компенсации реактивной мощности
Рисунок 6 Упрощенная схема компенсации реактивной мощности ,
,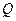 - величина реактивной мощности;
- величина реактивной мощности; - напряжение сети.
- напряжение сети.





