ОПРЕДЕЛЕНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ ТЕХНОЛОГИЧЕСКИХ ПАРАМЕТРОВ

Как уже было описано выше, контролируемым параметрами КЦ является давление газа на выходе. Этот параметр измеряется с помощью датчиков. Значения контролируемых параметров снимаемых с датчиков являются случайными величинами. Эти значения являются основными входными данными для обеспечения правильной и безаварийной работы всей АСУ, поэтому очень важно знать закон распределения измеряемых параметров.

Существует несколько законов распределения [10]: нормальный, усеченный нормальный, равномерный, логарифмический нормальный, экспоненциальный.

Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым. Применение нормального распределения можно обосновать по центральной предельной теоремы, которая гласит: каковы бы не были случайные величины , каждая из которых не превосходит существенно своим размахом остальных, в случае если число измерений велико, то сумма этих величин распределена асимптотически по нормальному закону.

Нормальное распределение являясь общим случаем распределения случайной величины в диапазоне , лишь в частности (при определенных условиях) может быть использовано для моделей надежности.

Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений контролируемых параметров. В общем случае усечение может быть: левым – ; двусторонним – (t₁ , t₂).

При изучении реальных измерений снимаемых с датчиков необходимо рассматривать закон усеченного нормального распределения для случая ограничения случайной величины значения технологического параметра интервалом (t₁ , t₂).

Плотность усеченного нормального распределения [10]:

,

где – случайная величина (измеряемый технологический параметр).

– параметры распределения (математическое ожидание и дисперсия).

c – нормирующий множитель, определяемый из условия, что площадь под кривой равна 1, откуда нормирующий множитель равен [10]:

 

,

где – функция Лапласа, представляющая распределение положительных значений случайной величины х в виде [10]:

 

На рисунке 5 представлена плотность усеченного нормального распределения.

Рисунок 5. Плотность усеченного нормального распределения

На рисунке 5: μ- наиболее вероятное значение давления масла; х₁ и х₂- случайные значения давления масла.

Критерий Вилкоксона - это непараметрический метод, который используется для оценки значимости различий двух связанных совокупностей количественных признаков.

Практический расчет критерия включает следующие этапы:

1) Найти разности парных вариант.

2) Определить ранги полученных разностей (без учета знаков, пары наблюдений, разности которых оказались равными нулю, из дальнейшей оценки исключаются).

3) Определить сумму рангов полученных разностей, имеющих одинаковые алгебраические знаки и взять меньшую из них (Т).

4) Установить достоверность различий. При количестве наблюдений меньше 26 сравнивают найденную сумму с критическими значениями из таблицы, в противном случае рассчитывают по специальной формуле случайную переменную.

Рассмотрим 2 датчика напряжения, которые служат для измерения напряжения на различных участках. Результаты сравнения датчиков сведены в таблицу 1.

Таблица 1. Показания датчиков давления масла.

Кол-во измерений	1 датчик	2 датчик	Разность	Ранги
	5,2		-0,8	7,5
	5,1	5,9	-0,7	7,5
	5,3	5,5	-0,2	1,5
	5,1	5,8	-0,7
	5,5	5,9	-0,4
	5,3	5,9	-0,6
	5,9	4,8	1,1
	5,4	4,9	0,5
	5,7	5,9	-1,2
	5,6	5,4	0,2	1,5

 

Сумма рангов со знаком «+» =4

Сумма рангов со знаком «-» = 7

Наименьшая сумма Т = 14,5,

Критическое значение Т по таблице для n = 11 (число пар)

 

.

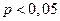
Поскольку не входит зону , то объединяемость двух выборок не может быть осуществлена. Напряжение, контролируемое двумя датчиками не может быть заменена на один датчик, в связи с непосредственной необходимостью измерения давления на разных участках.