Определение месторасположения склада
Для решения одной из фундаментальных логистических задач-определения месторасположения распределительного склада в регионе необходимо знать: · месторасположение (координаты xi, yi) фирм-производителей и потребителей (клиентов) данной продукции; · объемы поставок продукции (Qi); · маршруты доставки (характеристику транспортной сети); · затраты (или тарифы) на транспортные услуги (Ti). В зависимости от выбранного критерия оптимизации и учета расстояний между поставщиками, потребителями и складом рассматриваются следующие типовые случаи. Первый вариант [25 и др.]. Месторасположение распределительного склада определяется в виде координат центра тяжести грузовых потоков по формулам:
где: Ax, Ay - координаты распределительного склада, км; Qi - объем (вес) груза, т; xi yi - соответственно расстояние от начала осей координат до расположения поставщика или клиента, км. Второй вариант [20]. Месторасположение склада определяется как «центр равновесной системы транспортных затрат». Расчет координат склада производится по формулам:
где Ti - транспортный тариф для i-го поставщика или потребителя (клиента), руб.\т.км. Суммирование в формулах (8.1) - (8.4) производится от i = 1 до m, где m- общее количество поставщиков и потребителей. Очевидно, что при Ti =const., формулы (8.1), (8.2) и (8.3), (8.4) совпадают. С другой стороны, транспортные тарифы Ti в формуле (8.3), (8.4) играют роль весовых коэффициентов, которые могут принимать различные значения и, следовательно, расширяют возможности учета различных факторов по сравнению с формулами (8.1), (8.2). Однако, не следует забывать, что тарифы функционально связаны с грузооборотом (т.км) и объемом перевозок (т), поэтому их упрощенный учет в расчетных зависимостях требует дополнительного обоснования, либо введения более сложных зависимостей. Рассмотрим пример расчета координат склада по первому и второму вариантам. Исходные данные о координатах расположения поставщиков Пi и клиентов Кi приведены в табл.8.1; также представлены вспомогательные расчеты. При подстановке значений в формулы (8.1),(8.2) находим Аx = Ay = Второй вариант расчета, формулы (8.3), (8.4) дает Аx = Ay = Приведенные на рис.8.1 местоположение складов показывают, что в данном конкретном случае их координаты различаются незначительно.
Таблица 8.1 Определение координат склада
Рис.8.1 Расположение поставщиков П, клиентов К и складов: С1 - первый вариант; С2 - второй вариант. Третий вариант [23, 28]. Координаты склада определяются исходя из условия, что сумма расстояний от данных точек m с учетом спроса Qi до точки (x,y)- координат склада- была минимальной. Целевая функция записывается в виде:
где ai, bi - координаты i-го поставщика или потребителя. Принципиальное отличие третьего варианта заключается в том, что, во-первых, он сформулирован как классическая оптимизационная задача, во-вторых, расстояние между складом и другими объектами определяется как «гипотенуза», тогда как в задачах первом и втором вариантах рассматриваются расстояния по осям X и Y. Для нахождения координат склада используется аналитический метод, согласно которому на первом этапе определяется система из 2-х уравнений в виде частных производных функций P (x,y).
Поскольку решение данной системы затруднено, на втором этапе используется итерационный метод. Так первое приближение для x(1) рассчитывается по формуле:
Входящее в формулу
На третьем этапе значения x(1) подставляется во второе уравнение системы (8.6) для частной производной по Y и находится первое приближение для y(1). Затем y(1) подставляется в уравнение для частной производной по X и находится второе приближение x(2) и т.д. до тех пор, пока разница итераций P(k) (x,y) и P(k+1) (x,y) не станет меньше достаточно малого положительного числа E. Однако, попытка использовать описанный итерационный метод решения наталкивается на такие же трудности, как и аналитическое решение системы (8.6). Это нетрудно показать на следующем примере. Запишем в явном в виде первое уравнение системы (8.9).
Допустим, что m=2, ax(1) рассчитано по формуле (8.7) Тогда, для нахождения y(1) надо решить уравнение:
После преобразований получим кубическое уравнение для определения y(1): очевидно, что с увеличением m расчетные формулы усложняются, следовательно, использование итерационного подхода не упрощает поиск координат склада. Рассмотрим подход, основанный на непосредственном поиске минимума функции (8.5). Исходные данные для расчетов приведена в табл.8.1. Для примера рассчитаем величину транспортной работы при перевозках от производителей на склад и со склада клиентам, выбрав в качестве координат склада следующие значения: x1=250 км, y1 = 425 км. Тогда по формуле (8.5) для первого поставщика (а1 = 300 км, в1 = 575 км) находим:
Результаты расчетов Р(x1, y1) для всех поставщиков и клиентов приведены в табл. 8.2: Р(x1, y1)≈342 тыс.км
Таблица 8.2 Определение транспортной работы при координатах склада х1 = 250 км, у1 = 425 км
Расчеты были выполнены в виде трех блоков. В первый блок вошли расчеты для пяти точек (рис.8.2), координаты которых и результаты расчетов приведены в табл. 8.3. Анализ результатов позволил выявить направление поиска координат склада (второй блок, три точки), изменив его вдоль координаты х = 300 км. Наконец, минимальное значение транспортной работы оказалось равным Р = 329950 т.км. (при принятом в расчетах шаге ∆ = 25 км), что соответствует координатам склада: х = 300 км; у = 500 км.
Рис.8.2 Графическая интерпретация поиска минимума функции P (x, y): 342(1) – транспортная работа в тыс.км (номер варианта расчета в табл.8.3) Таблица 8.3 Определение координат склада (численный метод)
Следует подчеркнуть, что разница значений Р (х, у) между 6 и 7 вариантами составляет 0,46%, а между 9 и 7 – 0,1%. С одной стороны это затрудняет поиск минимума функции Р(х, у), с другой стороны говорит о том, что минимум Р(х, у) при заданном выражении целевой функции соответствует область значений, незначительно отличающихся друг от друга. Таким образом, с небольшой погрешностью координаты склада могут быть выбраны внутри этой области, что позволяет учесть всевозможные и часто противоречивые ограничения: административные, правовые и т.п. Заметим, что для поиска минимума Р(х, у) можно воспользоваться ускоренным алгоритмом, суть которого сводится к итерационному процессу расчета координат склада по формулам:
где
Вывод зависимостей (8.11), (8.12) покажем на примере первой из них. За основу берутся частные производные dP(x, y)/dx и dP(x, y)/dy, см. формулу (8.6). После суммирования, находим
Решая уравнение относительно Х, получим формулу, представляющую собой итерационное выражение
Таблица 8.4 Определение координат склада (первая итерация ускоренного алгоритма)
Расчет начинается с первого шага при При подстановке х0 = 300 км, у0 = 425 км по формулам (8.11), (8.12), рассчитываем значения сумм (табл.8.4) и находим первое приближение:
Второе приближение для координат склада:
Транспортная работа для второй итерации: Р( В заключение сопоставим варианты расчетов координат склада при использовании различных подходов, табл.8.5 Транспортная работа рассчитывалась по формуле (8.5), исходные данные для расчета приведены в табл. 8.1.
Таблица 8.5
|

 , (8.1)
, (8.1) , (8.2)
, (8.2) , (8.3)
, (8.3) , (8.4)
, (8.4) км,
км,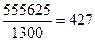
 км.
км. км,
км,

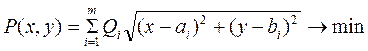 (8.5)
(8.5)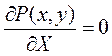 ;
;  (8.6)
(8.6) (8.7)
(8.7) определяется из уравнения
определяется из уравнения (8.8)
(8.8) (8.9)
(8.9) (8.10)
(8.10) т.км.
т.км. км
км

 , (8.11)
, (8.11) , (8.12)
, (8.12) (8.13)
(8.13)
 (8.14)
(8.14) и
и  , определяемых по формулам (8.1), (8.2) для координат «центра тяжести»
, определяемых по формулам (8.1), (8.2) для координат «центра тяжести» =
=  303 км;
303 км;  =
=  =440 км
=440 км = 305 км;
= 305 км;  = 460 км
= 460 км ,
, 


