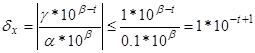Ошибки округления

При отсутствии ошибок ограничения и ошибок, вызванных погрешностью в исход­ной информации, вычисле­ния, выполняемые на ЭВМ, нельзя считать абсолютно точными, поскольку в ходе машинных вычислений возникают ошибки окру­гления. Попробуем разобраться в их природе.

В подавляющем большинстве научных и инженерных расчетов используются действительные числа, поэтому их сумма, разность, произведение и частное также являются действительными числами. Поскольку ЭВМ оперирует числами с конечным числом знаков и результат арифметической операции над вещественными числами округляется, возникают ошибки округления.

Будем действительное число представлять в нормализованном виде, т. е. в виде правильной дроби, называемой мантиссой, умноженной на целую степень 10, называемую порядком. Например,

15.392 = 0,15392*10²; 0.0541 = 0.54*10^-1.

Обозначим мантиссу некоторого числа х через a, а порядок - через b. Тогда х = a *10 ^b, где 0,1 <=½ a ½<1.

При выполнении сложения или вычитания ЭВМ выравнивает порядки, т. е. сдвигает мантиссу меньшего по абсолютной величине числа вправо или влево на столько разрядов, на сколько пришлось увеличить или уменьшить порядок меньшего числа:

0,123*10³ +0,453*10¹ = 0,123*10³ + 0,00453*10³ = 0,12753*10³.

Предположим, что мантисса может представляться только тремя значащими цифрами. Представим полученную сумму в виде суммы двух вещественных чисел: 0,12753*10³ = 0,127*10³ +0,53*10°.

Результат любого из четырех арифметических действий можно представить в общем виде следующим образом: х = a *10 ^b +g*10 ^b-t ,

где 0,1 <= | a | < 1; 0 < | g | < 1; t — число значащих цифр в мантиссе.

Существуют два способа округления результата арифметичес­кой операции. В первом случае g просто приравнивается нулю, а во втором случае к a прибавляется единица младшего разряда, если g по абсолютной величине больше или равна 0,5; если |g| << 0,5, то a остается без изменения.

Рассмотрим ошибку, появляющуюся при первом и втором спо­собах округления.

При первом способе округления величина относительной по­грешности будет равна

т. е. при этом способе округления относительная погрешность не зависит от полученного результата, а определяется количеством значащих цифр в ячейке памяти ЭВМ.

При втором способе округленный результат записывается сле­дующим образом:

В этом случае абсолютная погрешность не превышает 0,5*10 ^b-t, а относительная погрешность не будет превышать

 

Как видим, предельная ошибка округления при втором спо­собе меньше в два раза.

Как правило, известен лишь верхний предел возможной ошибки, поэтому при анализе точности вычислений на ЭВМ сле­дует предполагать наихудший вариант: равенство ошибки округ­ления своему верхнему пределу.