Основные сведения из теории. 1. Уравнения OУ, закон управления и схема набора СПС.
Им. Д. Ф. УСТИНОВА
Кафедра «Системы обработки информации и управления»
Б.Р. АНДРИЕВСКИЙ, В. Ю. ЕМЕЛЬЯНОВ, Б. Ф. КОРОТКОВ
ТЕОРИЯ УПРАВЛЕНИЯ Лабораторный практикум В среде Scilab
Санкт-Петербург
Теория управления:Лабораторный практикум в среде Scilab / Б.Р. Андриевский, В. Ю. Емельянов, Б.Ф. Коротков; Балт. гос. техн. ун-т; СПб., 2010. 45 с.
Посвящен вопросам синтеза линейных непрерывных и дискретных систем, анализу нелинейных систем и систем с переменной структурой. Содержит основные сведения из теории, описание используемых моделей, руководство по выполнению работ на персональном компьютере в программной среде Scilab/Scicos с вариантами индивидуальных заданий, перечень рекомендуемой литературы. Предназначен для студентов специальностей 160403, 230102, 230201.
Ил. 19. Табл. 7.
Рецензент
Утверждено редакционно-издательским советом университета
Ó БГТУ, СПб, 2010
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ОСНОВНЫХ МЕТОДОВ ПОВЫШЕНИЯ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы – сравнительный анализ различных методов повышения точности САУ.
Основные сведения из теории
К числу важнейших показателей качества систем автоматического управления (САУ) относится установившаяся (статическая) ошибка – величина ошибки управления x (t)= g (t) –y (t) в установившемся процессе. Здесь g (t) – задающее воздействие, y (t) – выход системы. Установившаяся ошибка САУ может быть измерена по окончании переходного процесса или рассчитана. Для линейной системы при известных структуре, параметрах и задающем воздействии используется теорема о конечном значении:
где Ф x (s) – передаточная функция замкнутой системы по ошибке, G (s) – изображение по Лапласу задающего воздействия. При одновременном действии на систему нескольких сигналов используется принцип суперпозиции:
где xg, xf – составляющие статической ошибки, определяемые задающим и возмущающим воздействиями; Если главная обратная связь в системе единичная и отрицательная, соотношение (1) принимает вид
где W (s) – передаточная функция разомкнутой системы, Wf (s) – передаточная функция разомкнутой системы по возмущающему воздействию. Если система является статической как по задающему, так и по возмущающему воздействиям, то при g (t) =g 01(t)и f (t) =f 01(t) формула (2) позволяет получить
где K – общий коэффициент усиления по разомкнутой цепи, kf – коэффициент передачи от точки приложения возмущения f (t) до выхода системы y (t). Из выражения (3) следует, что величина ошибки статической системы может быть уменьшена при увеличении общего коэффициента усиления. Однако это увеличение связано с уменьшением запаса устойчивости системы. Поэтому одновременно с увеличением коэффициента K необходимо вводить в САУ корректирующие (демпфирующие) средства. Разработаны и другие методы повышения точности: 1) повышение порядка астатизма, что соответствует введению в систему интегрирующих или изодромных звеньев; 2) введение производной от ошибки в закон управления; 3) введение неединичных обратных связей; 4) применение комбинированного управления.
1.1. Описание исследуемой системы
В работе исследуется система управления, структурная схема которой изображена на рис. 1. Нескорректированная система состоит из трех последовательно включенных апериодических звеньев. К системе приложено задающее воздействие g (t) =g 0×1(t), на объект управления также действует возмущающее воздействие f (t) =f 0×1(t).
На структурной схеме пунктиром показаны дополнительные звенья, которые вводятся в систему с целью повышения ее точности: 1) прямое параллельное корректирующее устройство с коэффициентом передачи k п, позволяющее ввести производную от ошибки в закон управления; 2) вспомогательное дифференцирующее звено с коэффициентом передачи k' ос, позволяющее реализовать гибкую обратную связь; 3) интегрирующее звено с коэффициентом передачи k и, позволяющее повысить порядок астатизма системы; 4) изодромное звено с коэффициентами передачи k и и k' и, позволяющее повысить порядок астатизма системы без существенной потери запаса устойчивости; 5) вспомогательное звено с коэффициентом передачи k ос, позволяющее реализовать цепь основной обратной связи с коэффициентом передачи, отличным от единицы; 6) дополнительное звено с коэффициентом передачи k в, позволяющее вводить на вход системы сигнал, пропорциональный возмущению f (t), с целью компенсации последнего, и тем самым создать комбинированную систему управления.
1.2. Нескорректированная система
Исходная система является статической и состоит из трех последовательных апериодических звеньев, охваченных единичной обратной связью (k ос=1). Передаточная функция разомкнутой системы
где K 0= k 1 k 2 k 3 – общий коэффициент усиления. Нетрудно убедиться, что исходная САУ является статической как по задающему, так и по возмущающему воздействиям, и для нее справедливо соотношение (3). Оценим возможность повышения точности нескорректированной системы путем увеличения коэффициента K 0. Основная передаточная функция нескорректированной замкнутой системы:
Характеристический полином нескорректированной замкнутой системы:
Используя критерий устойчивости Гурвица, можно определить условия устойчивости замкнутой САУ и критическое значение коэффициента K 0, при котором нескорректированная САУ будет находиться на колебательной границе устойчивости. В случае характеристического полинома третьей степени для анализа устойчивости достаточно рассмотреть определитель второго порядка:
Условием устойчивости является неравенство Δ2>0, откуда K 0 <K 0кр, где Поэтому возможность повышения точности исследуемой САУ лишь за счет увеличения коэффициента усиления разомкнутой системы ограничена, причем максимально допустимое значение K 0 должно быть меньше K 0кр в соответствии с требуемым запасом устойчивости системы.
|

 ,
,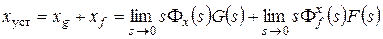 , (1)
, (1) – передаточная функция замкнутой системы по ошибке от возмущающего воздействия; F (s) – изображение по Лапласу возмущающего воздействия f (t).
– передаточная функция замкнутой системы по ошибке от возмущающего воздействия; F (s) – изображение по Лапласу возмущающего воздействия f (t). , (2)
, (2) , (3)
, (3)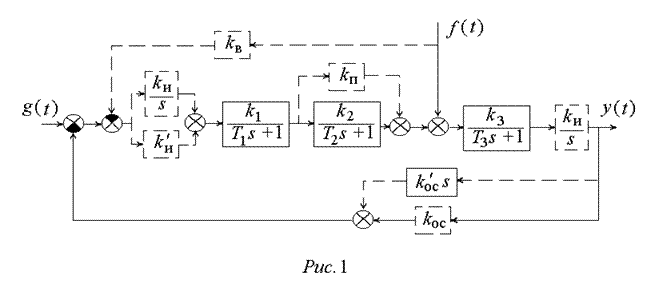
 ,
, . (4)
. (4) .
. .
.



