Производственный выбор фирмы в долгосрочном периоде. Изокванты. Предельная норма технологического замещения. Взаимозаменяемость факторов производства.

 

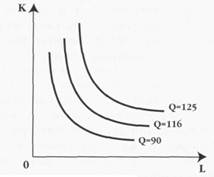
Изокванты обладают следующими свойствами:

• изокванты никогда не пересекаются в силу действия принципа тран­зитивности.[81] Каждой изокванте соответствует определенный объем выпус­ка продукции, причем, чем дальше изокванта отстоит от начала коорди­нат, тем больший объем выпуска обеспечивается;

- изокванты имеют отрицательный наклон. Это объясняется тем, что для сохранения неизменным объема выпуска продукции при уменьшении использования одного фактора необходимо увеличить применение другого фактора;

• изокванты становятся более поло­гими по мере продвижения сверху вниз вдоль них. Это связано с тем, что в верх­ней части изокванты, как видно на рис. 10.4, для выпуска заданного объема про­дукции используется большое количество капитала и незначительное количество труда. При движении вниз вдоль изокван­ты требуется все больше единиц труда для замещения каждой единицы капитала, вследствие падения пре­дельной производительности труда по мере наращивания его количе­ства. Этим объясняется выпуклая по отношению к началу координат форма изоквант.

 

 

Рис. 10.4. Карта изоквант

С помощью наклона изоквант можно определить степень замещения одного фактора производства другим. Например, фирма производит продукцию с использованием двух переменных факторов: капитала (К) и труда (L). Начнем двигаться вниз по изокванте с объемом выпуска про­дукции, равным 116 ед. (см. рис. 10.4), сокращая количество применяе­мого капитала. Для того чтобы остаться на этой изокванте, т. е. обеспе­чить тот же объем производства, фирме потребуется увеличить количе­ство применяемого труда. Отношение изменения в количестве одно­го фактора к изменению в количестве другого фактора при сохра­нении неизменным объема производства называется предельной нормой технологического замещения (MRTS).

MRTS_KL = ΔK/ΔL (9)

В нашем примере MRTS представляет собой пропорцию замещения капитала трудом при условии, что мы остаемся на той же самой изо­кванте с объемом в 116 ед.

Как известно, наклон кривой в каждой точке определяется наклоном касательной в данной точке, который, в свою очередь, равен отношению величины изменения фактора К к величине изменения фактора L (ΔK/ΔL.). Это означает, что наклон изокванты равен предельной норме технологического замещения. В силу того, что изокванта имеет отрицательный наклон, MRTS_KL в любой точке будет равна наклону касательной в данной точке, умноженной на —1, т. е.

MRTS= ΔK/ΔL х (-1) (10)

 

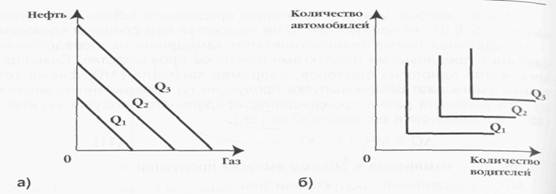
Если вы хорошо усвоили категорию предельной нормы замещения MRS (гл. 5, § 9), то понятие MRTS не покажется вам слишком сложным.

Предельная норма технологического замещения непосредственно связана с предельными продуктами факторов производства. Сокращая количество одного из факторов, например капитала (ΔK), фирма тем самым уменьшает объем выпуска продукции на определенную величи­ну Эта величина равна произведению предельного продукта капитала MP_к и изменения в его количестве (ΔK):

ΔQ = МР_kх (-ΔК) (11),

где ΔQ - изменение в объеме выпуска продукции;

МР_К- предельный продукт капитала;

ΔК - изменение количества применяемого капитала.

Для того, чтобы остаться на той же изокванте, сокращение объема производства должно быть компенсировано увеличением количества применяемого труда (ΔL), т. е.

ΔQ = MP_Lx ΔL (12),

где MP_L- предельный продукт труда; AL -изменение количества применяемого труда. Это означает, что абсолютное значение ΔQ в уравнениях (11) и (12) должно быть одинаковым. Следовательно, можно записать:

МР_кх (-АК) = MP_Lx AL (13)

Отсюда следует, что

MRTS_KL = - ΔК / Δ L = MP_L / MP_K = наклону изокванты (14)

Как видно из рис. 10.4., изокванты имеют выпуклую по отношению к началу координат форму. Это связано с тем, что по мере движения вниз по изокванте MRTS_KL уменьшается. Объясняется этот факт следующим образом: по мере увеличения количества фактора L его предельный продукт уменьшается относительно предельного продукта фактора К. Соответ­ственно, сокращение применяемого фактора К ведет к росту его пре­дельного продукта. Это означает, что знаменатель в уравнении (14) будет расти, а числитель будет уменьшаться. Следовательно, MRTS_KL будет снижаться.

Изокванты могут иметь различный вид в зависимости от степени взаиимозаменяемости ресурсов. Рассмотрим три случая. И вновь нам поможет аналогия с взаимозаменяемостью товаров при анализе различной конфигурации кривых безразличия (гл. 5, § 9).

Ресурсы могут обладать абсолютной взаимозаменяемостью. Это означает, что заданный объем выпуска продукции может быть обеспечен как путем использования какого-либо одного из двух переменных ресурсов, так и путем их комбинаций. В этом случае изокванта будет иметь вид пря­мой линии (см. рис. 10.5а), a MRTS будет постоянной величиной. Напри­мер, нефть и газ, как сырье для получения энергии, являются абсолютно взаимозаменяемыми.

Второй случай - ресурсы обладают свойством абсолютной ком-плементарности.Это означает, что два переменных ресурса, исполь­зуемых для производства данного вида продукции, имеют одну опреде­ленную пропорцию. Иначе говоря, заданная производственная функция предполагает наличие единственно возможной комбинации ресурсов. Е этом случае MRTS будет равна 0, а изокванта будет иметь вид прямого угла, как это изображено на рис. 10.56. Обязательным условием пере­хода на более высокую изокванту такого вида является соблюдение за­данной пропорциональности в использовании ресурсов. Если будет уве­личено количество одного ресурса без соответствующего изменения в

 

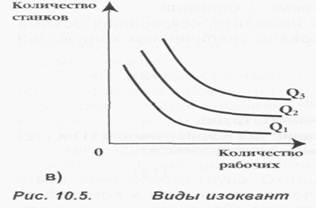
количестве другого, то перейти на другую изокванту не представляется возможным. В качестве примера такой производственной системы можно привести сферу транспортных услуг. Для обеспечения роста объема слуг необходимо увеличение в пропорции один к одному как автомо­бильного парка, так и численности водителей при условии односменно­го режима работы. Еще более простой пример: для уборки улицы фир­ма по предоставлению жилищно-коммунальных услуг может нанять 1 дворника, снабдив его одной метлой. Сочетание 20 дворников и 1 мет­лы экономически бессмысленно, так же, как и сочетание 1 дворника и 20 метел. Переход на более высокую изокванту в данном случае остав­ляет неизменной пропорцию 1:1, например, 3 дворника и 3 метлы.

И, наконец, третий случай (рис. 10.5в) - изокванты, отражающие ча­стичную взаимозаменяемостьресурсов. В этом случае производство продукции может осуществляться с обязательным использованием двух переменных ресурсов, например, труда и капитала. Однако их комбина­ции могут быть самыми различными в соответствии с заданной произ­водственной функцией. Данная форма изоквант встречается чаще все­го, и ее принято считать стандартной.