Массаларды келтіру және инерция моменттері

Зерттелетін механизмдер схемасының динамика жұмысын шешу үшін, оларды өзара серпімді элементтермен жалғанған жеке элементтер түрінде қарастырған жөн.

Нақты механизмнің элементтер массасын т„ т_:,т,..., ал қозғалыс жылдамдығын V₁,V₂,V₃, арқылы белгілейді. Массаларды динамикалық келтіру шарты келтірілген массаның кинетикалық радиусы мен нақты механизмнің барлық массасының теңдігі болып саналады.

 

 

г)

д)

е)

а — бірмассалық; в — екімассалык; г - үшмассалық; д — таралған массамен; е — моменттерді келтіру үшін есептік схема мысалы

30 сурет - Есептеу схемасының мысалдары

 

31 сурет - Кіру-қозғалыс жүйесінің есептік схемасы

 

Егер массаларды белгілі бір жылдамдықпен V₀ қозғалатын массаның қосылатын нүктесіне келтірсе, онда:

осыдан:

мұнда m_n -механизмнің барлық элементтерінің келтірілген массасының мәні.

Мынаны ескере отырып:

аламыз

 

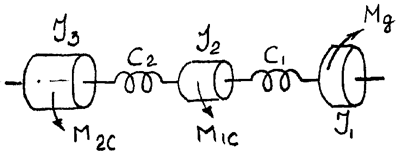
Яғни, келтірілген масса келтірілген массалар қосындысының берілетін қатынастың квадратына бөлінген суммасына тең.

Егер механизм схемасында айналмалы массалар болса, онда жеке массалар инерциясының моменттерін келтіруді осыған ұқсас жүргізеді (32 сурет үшін).

32 сурет - Айналдырғыш жүйесінің есептік схемасы

 

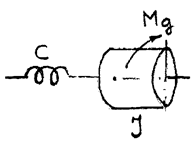
Егер механизм қозғалмалы келетін және айналмалы элементтерден тұрса (33 сурет), массаны инерция моменті арқылы, ал инерция моментін масса арқылы көрсету керек.

33 сурет —Келу-козғалмалы да және айналмалы да элементтері бар жүйенің есептік схемасы

 

Барабан осіне келтірілетін инерция моменті арқылы көрсетілген жүк массасы мынаған тең: Келтірілген барабан жүгінің инерция моменті:

Егер барабанның инерция моментін масса түрінде көрсетсе және жүкке келтірсе, онда:

Ал толық келтірілген барабан мен жүктің массасы мынаған тең болады:

Динамиканың жұмыстарын шамамен шешу үшін, кейде шаршыранды массаларды шоғырланған массалар түрінде көрсеткен дұрыс.

Бұл жағдайда келтіру тәсілін қолдануға да болады.

Дебиет

9 негізгі /7-12/