Лекция Технологиялық жүктемеден болатын машиналардағы динамикалық жүктемелер
Механизмнің ең қарапайым екімассалық эквиваленттік схемасы үшін (35 сурет) өтпелі кезеңдегі масса қозғалысының дифференциалдык тендеуін келесі түрде көрсетуге болады:
мұнда J1- жетектің бірінші массасының инерция моменті: J2 - электрқозғағыш білігіне келтірілген, механизмнің екінші инерция моменті; с12 - жетек берілісі желісіне келтірілетін қаттылық: τ - уақыт; φ1, φ2 - массаның, радтың бұрыштық ауытқуы; М1 - қозғағыш моменті; М2 - электрқозғағыш білігіне келтірілген жұмыстағы машинаның технологиялық кедергісі (минус белгісімен).
35 сурет — Механизмнің екімассалық эквиваленттік схемасы
(59) және (60) теңдеулердегі бірінші қосынды — сәйкес масса инерциясы күшінің моменті, екіншісі - жетектер байланысындағы серпімділік күшінің моменті; тендеудің оң жағындағы — механизмнің жұмыс бөлігіндегі қозғағыш пен технологиялық кедергіге сәйкес сыртқы күш моменті. Динамикалық процестердің сипаты және тербелісамплитудасының шамасы жүйе параметрлеріне, жетектің технологиялық кедергі күшімен М2 жүктелу заңына және М1. қозғағышының жұмысына байланысты. Технологиялық өндіріс машиналарының кедергі күші технологаялық пайдалану ерекшелігімен анықталады. Кейбір технологиялық машиналардыің технологиялық кедергі күшімен жүктелуінің жиі кездесетін жағдайларына тоқталайық. Технологиялық жүктемелердің динамикалық жүктеме қарқынына әсері, машинаның екімассалық эквиваленттік моделі мысалында қарастырайық. Бірінші және екінші массалық байланыстар арасындағы серпімділік іс күшінің моменті:
тең екенін ескере отырып, дифференциалдық тендеулерді (59) және (60) мына түрде жазуға болады:
а.Электркозғағыштың тұрақты моментінің әсері кезінде жүйеге технологаялық кедергі моментін бірден салу. Дифференциалдық тендеуді (62) бастапқы нөлдік жағдайда τ=0; М12=0;
мұнда М а - екінші массаның статистикалық кедергі күшінен және инерциясынан болатын суммарлық момент;
мұнда ε орташа бұрыштық жылдамдык; υ - жүйенің меншікті тербелісінің жиілігі, 1/с;
Тербеліс кезеңдері. с,
Динамикалық жүктемелерді сипаттау үшін динамикалық коэффициент қолданады, ол динамикалық жүктеменің максималды мәнінің тұрақты (немесе статистикалық) жүктемеге қатынасына тең:
(64) және (66) формулалардан екімассалық жүйенің тұрақты моменттермен жүктемеленген жағдайында динамикалық коэффициент 2 тең болатыны анықталды. Үйкеліс және энергияның таралуы салдарынан тербеліс уақыт өткен сайын сөнеді. Динамикалық коэффициент жүктелу күші функциясының түріне, олардағы өсу жылдамдығына, жерлерде саңылаудың болуына және басқа факторларға байланысты. б.Технологиялық момент желістік заң бойынша өседі, содан кейін түрақгы болып кдлады (36 а сурет):
М2=Мс при τ≥τ0,
мұнда τ0 - жүктеменің өсу үзақтығы. Серпімді байланыстағы динамикалык жүктеме:
мұнда М п - және кезеңдік (В) өсу заңдылығы а - жүктеме графигі; б - динамикалық коэффициент Динамикалық коэффициент:
мұнда
33 А суретте бұл қисық пунктирмен көрсетілген.
36 сурет - Металлургиялык жүктеменің сызыктық, (А), экспоненциалдық (Б)
λ;. өскен сайын динамикалық коэффициент азаяды және λ;>5 кезінде, ол бар болғаны бірліктен бірнеше пайызға көп болады; бұл жағдайда динамикалық коэффициентті ескеруге болады. в. Техникалық жүктеме экспоненциалдық заң бойынша өседі (2,39,Б сурет).
мұнда А — экспененттер көрсеткіші. Бастапқы нөлдік жағдайда жетек желісіндегі серпімділік күші моментінің теңдеуі мына түрде болады:
мұнда λ=υА; γ= аrс(–λ). Динамикалық коэффициент:
А жүтемесінің экспоненттік өсу көрсеткіші аз болған сайын (36,Б сурет), жетектің серпімді жүйесіне келетін динамикалық әсер көп болады. Аυ>10 кезінде динамикалық коэффициенттің бірліктен айырмашылығы өте аз, яғни машинаға тек статистикалық жүктеме түседі деуге болады. г. Кезеңді жүктеме (36, В сурет). Сөнетін меншікті тербелістен басқа, күшті қоздыратын кезеңді әсерлер, тұрақты еріксіз тербелістер тудырады. Тербелетін массаның (жұмыс бөлігі) қозғалыс жылдамдығына пропорционал тұтқыр кедергіні ескере отырып, тербеліс процесін қарастырайық. Жұмыс бөлігі қозғалысының теңдеуі:
мұнда а - демпфирлеу коэффициенті, Н.м.с. Ротордың бұрылу бұрышын уақыт функциясымен. φ1=ωτ. көрсетейік. Тендеудің жалпы шешімі біртекті теңдеуді шешуден және жеке шешімнен тұрады:
мұнда Байланыстағы серпімділік күшінің моменті:
немесе:
мұнда Динамикалық коэффициент
Тендеудегі (1.36) бірінші қосынды υ жиіліктегі сөнетін бос тербелісті сипаттайды, соңғысы – ω жиіліктегі козу күшінің әсеріндегі еріксіз тербеліс. Тербелістің сөну қарқыны тербелістің логарифмдік декрементімен сипатталады:
мұнда Аk және Аk+1 - көрші тербеліс амплитудасының мәні. Логарифмдік декрементті, әдетте бірліктің бірнеше жүздіктен ондық бөлігіне дейін құрайды; салыстырмалы түрде үлкен сөнуде, әрбір келесі амплитуда алдыңғысынан екі рет кіші болғанда, δ=ln2=0,693. Меншікті және еріксіз тербелістер бірдей болған жағдайда, жүйеде жаңғырықты режим пайда болады, бүл кезде жетектегі серпімділік күші моменттің амплитудасы, кедергінің диссипативтік күштің әсері нәтижесінде шектеледі. Демек, демпфирленген жүйеден динамикалық коэффициент энергетикалық сипаттамаға а /(Jυ) байланысты, Динамикалық коэффициенттің максималды мәні жаңғырық кезінде болады (ω/υ=1) және kд=Jυ/ а тең. д. Күштің импульстік әсері. Технологиялық машиналар көбіне импульс типіндегі күшпен жүктеледі (37 сурет).
а — төртбұрышты импульс; б — жартылай синусоидалды импульс; в — көрсетілген импульстар (а,б) үшін динамикалық коэффициент 37 сурет — Импульстік жүктеме
Серпімді жүйеге қозу күшінің динамикалық әсеріне жалпы түрде бағаны А.Н.Крылов берді. Жүйеге статистикалық жүктемеден басқа күштің әсері кезінде, күштің өсу жылдамдығына және жүйенің меншікті тербеліс кезеңіне байланысты динамикалық жүктеме туады. Қозушы күштің кисығында бір максимум және Р(О)..О болса, онда А.Н.Крылов бойынша былай жазуға болады:
мұнда τ0 - ауыспалы, ол интеграция жүргізілетін 0-ден τ;, -ге дейін өзгереді; Т - жүйенің бос тербеліс кезеңі. Формуланың (1.38) оң жағында бос тербеліс кезеңінің уақыттық қозу күшінің қосымша өсуінің максималды мүмкіндігі келтірілген. Динамикалық тиімділік Т серпімді жүйесінің меншікті тербелісі кезеңінің және θ; сыртқы күш әсерінің ұзақтығының қатынасымен бағаланады. Егер күштің әсерлік ұзақтығы Т тербелісінің меншікті кезеңімен салыстырғанда көп болса, онда жүйедегі динамикалык жүктеме аз болады және оларды ескермеуге болады; жүйе статистикалык күшпен жүктеледі. Тез жоғалатын күш әсері кезінде, олардың әсерлік ұзақтығы θ - Т тербелісінің меншікті кезеңімен салыстырғанда аз болса, динамикалық жүктеме θ/Т. қатынасымен анықталады. Тікбұрышты және жартылай синусойдалды заң бойынша, жүйеге өте қысқа уақытқа козушы күш әсер етті делік. Серпімді байланыстың бастапқы нөлдік шарты үшін τ>;0 кезіндеп жүктеменің бірінші заңы бойынша динамикалық күш мынаған тең:
υθ/2=πθ/Т=πλ; белгілеп, динамикалық коэфициенттің мәнін аламыз: kд=2sinπλ; (80) мұнда λ - жүктеме параметрі. Жүктеме параметрінің функциясындағы динамикалық коэфициент графиктің өзгерісі 37, б суретте көрсетілген. Егер күш меншікті тербеліс кезеңінің аз бөлігінде әсер етсе, онда ондай күш аз және тіпті үлкен жүктеме әсері серпімді жүйе үшін қауіпті емес екендігін графиктен көруге болады. Жүйенің өте аз уақыттық жүктемесінде (θ<Т/2) максималды динамикалық әсер сырткы күш жойылғаннан кейін-ақ көрінеді. Қысқа уақыттық күш әсерінде динамикалық коэфициент, тек күш әсері мен жүйенің меншікті тербелісі кезеңдерінің қатынасымен ғана емес, сонымен бірге, жүктеме функциясына да байланысты болады. Тікбұрышты импульстен бөлек жүктеме, динамикалық тиімділікті жұмсартады (37,в суретті қараңыз). Дебиет 2 негізгі /75-83/
|

 ; (59)
; (59) ; (60)
; (60)
 , (61)
, (61) . (62)
. (62) , шешіп, жетектегі серпімділік күш моменті үшін мына түрде формула аламыз:
, шешіп, жетектегі серпімділік күш моменті үшін мына түрде формула аламыз: , (63)
, (63)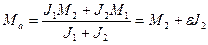 ; (64)
; (64) .
. . (65)
. (65) .
. (66)
(66) τ<τ0 кезінде (67)
τ<τ0 кезінде (67) , (68)
, (68)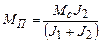 моменттерінің тұрақты құрастырушылары; ψ; - фазалық бұрыш.
моменттерінің тұрақты құрастырушылары; ψ; - фазалық бұрыш. , (69)
, (69) - жүктеменің өсу уақытының жүйенің меншікті тербеліс кезеңіне қатынасы τ;≥0,5Т жағдайы үшін кейбір жорамалмен мынаны жазуға болады:
- жүктеменің өсу уақытының жүйенің меншікті тербеліс кезеңіне қатынасы τ;≥0,5Т жағдайы үшін кейбір жорамалмен мынаны жазуға болады: . (70)
. (70)


 , (71)
, (71) . (72)
. (72) . (73)
. (73) , (74)
, (74)
 , (75)
, (75)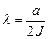
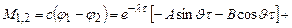
 , (76)
, (76) ,(1.36)
,(1.36)
 . (77)
. (77) ,
,

 , (78)
, (78) . (79)
. (79)


