Сформулировать принципиальные отличия сплайн- интерполяции от интерполяционной формулы Лагранжа.
В основе сплайн-интерполяции лежит следующий принцип. Интервал интерполяции разбивается на небольшие отрезки, на каждом из которых функция задается полиномом третьей степени. Коэффициенты полинома подбираются таким образом, чтобы выполнялись определенные условия (какие именно, зависит от способа интерполяции). Общие для всех типов сплайнов третьего порядка требования - непрерывность функции и, разумеется, прохождение через предписанные ей точки. Дополнительными требованиями могут быть линейность функции между узлами, непрерывность высших производных и т.д. Основными достоинствами сплайн-интерполяции являются её устойчивость и малая трудоемкость. Системы линейных уравнений, которые требуется решать для построения сплайнов, очень хорошо обусловлены, что позволяет получать коэффициенты полиномов с высокой точностью. В результате даже про очень больших N вычислительная схема не теряет устойчивость. Построение таблицы коэффициентов сплайна требует O(N) операций, а вычисление значения сплайна в заданной точке - всего лишь O(log(N)). Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа. 29. Функция 'nearest' — линейная интерполяция (принята по умолчанию); Пример (интерполяция функции косинуса): » x=0:10:y=cos(x); » xi=0:0.1:10; » yi= nearest (x,y,xi); » plot(x,y,'x',xi,yi,'g'),hold on » yi= nearest (x,y,xi.'spline'): » plot(x,y,'o ' ,xi,yi,'m').grid,hold off
30. Функция 'linear' — линейная интерполяция (принята по умолчанию); Пример (интерполяция функции косинуса): » x=0:10:y=cos(x); » xi=0:0.1:10; » yi= linear (x,y,xi); » plot(x,y,'x',xi,yi,'g'),hold on » yi= linear (x,y,xi.'spline'): » plot(x,y,'o ' ,xi,yi,'m').grid,hold off
31. Вычислить значение интеграла Для вычисления значений определенных интегралов в пакете MATLAB имеются следующие функции quad(), quadl(), trapz(), cumtrapz(). Функция trapz() вычисляет интеграл, используя метод трапеций. Синтаксис функции trapz(): Z = trapz(Y) % возвращает значение определенного интеграла, в % предположении, что X=1:length(Y) Z = trapz(X,Y) % возвращает значение интеграла % на интервале [X(1),X(N)] Z = trapz(...,dim) % интегрирует вектор Y, формируемый из чисел, % расположенных в размерности dim % многомерного массива Пример 6.4. Вычисление определенного интеграла >> x=0:0.01:pi/2; % задание координат узловых точек >> y=sin(x); % вычисление значений подынтегральной функции в % узловых точках >> trapz(y) % вычисление значения интеграла, в предположении о % том, что шаг интегрирования равен единице ans = 99.9195 >> trapz(x,y) % вычисление значения интеграла на отрезке % шагом интегрирования 0.01 ans = 0.9992 32. Вычислить значение интеграла Для вычисления значений определенных интегралов в пакете MATLAB имеются следующие функции quad(), quadl(), trapz(), cumtrapz(), которые имеют следующий синтаксис. >> q = quad(fun,a,b) % возвращает значение интеграла от функции % fun на интервале [a,b], при вычислении % используется адаптивный метод Симпсона. Пример 6.3. Вычисление интеграла >> q=quad('sin',0,pi/2,10^-4) q = 1.0000 >> q-1 ans = -3.7216e-008 >> q=quad('sin',0,pi/2,10^-6,'trace'); E-001 0.0896208493 E-001 0.4966040522 E-001 0.2032723690 E-001 0.2933317183 E-001 0.4137750613 >> q-1 ans = -2.1269e-009 >> [q,fnct]=quad('sin',0,pi/2,10^-6,'trace'); E-001 0.0896208493 E-001 0.4966040522 E-001 0.2032723690 E-001 0.2933317183 E-001 0.4137750613 >> 17 33. Вычислить значение интеграла Пример 6.2. Вычисление интеграла >> f=inline('sin(x)'); % задание подынтегральной функции >> Xmin=0; >> Xmax=pi/2; >> N=2001; >> i=1:N; >> dx=(Xmax-Xmin)/(N-1); % шаг интегрирования >> x=Xmin:dx:Xmax; % вычисление координат узлов сетки >> y=feval(f,x); % вычисление значений функции в узлах сетки % вычисление интеграла по формуле левых прямоугольников >> m=1:N-1; >> y1(m)=y(m); >> Fl=sum(y1)*dx Fl = 0.9996 >> Fl-1 ans = -3.9295e-004
34. Вычислить значение интеграла Пример 6.2. Вычисление интеграла >> f=inline('sin(x)'); % задание подынтегральной функции >> Xmin=0; >> Xmax=pi/2; >> N=2001; >> i=1:N; >> dx=(Xmax-Xmin)/(N-1); % шаг интегрирования >> x=Xmin:dx:Xmax; % вычисление координат узлов сетки >> y=feval(f,x); % вычисление значений функции в узлах сетки % Нахождение значения интеграла с помощью %метода средних прямоугольников I=inf; for i=1:n-1 I=I+fz1(a+i*h+h/2); end format long e I1=I*h D1=abs(I-I1)
35. Аналитически найти теоретическую погрешность при численном вычислении интеграла Для нахождения зависимостей погрешности вычисления определенного интеграла на отрезке
Тогда интеграл от данной функции на отрезке
Оценим погрешность метода левых прямоугольников. Погрешность интегрирования
Из (6.24) видно, что основной член погрешности на каждом отрезке имеет порядок N, а
36. Аналитически найти теоретическую погрешность при численном вычислении интеграла Рассмотрим подробно один и возможных способов оценки погрешности формул численного интегрирования на примере метода средних прямоугольников. Для этого запишем выражение для интеграла на отрезке Для оценки погрешности интегрирования
В малой окрестности точки x в разложении (4.26) можно ограничится небольшим количеством членов ряда. Поэтому, подставляя в (4.25) вместо функции
При интегрировании и подстановке пределов получаем, что все интегралы от членов ряда (4.26), содержащих нечетные степени Главный член полной погрешности для интеграла на всем интервале
Формула (4.29) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, эта оценка является априорной, так как не требует знания значения вычисляемого интеграла. Степень шага h, которой пропорциональна величина 37. Вычислить значение интеграла Пример 6.2. Вычисление интеграла >> f=inline('sin(x)'); % задание подынтегральной функции >> Xmin=0; >> Xmax=pi/2; >> N=2001; >> i=1:N; >> dx=(Xmax-Xmin)/(N-1); % шаг интегрирования >> x=Xmin:dx:Xmax; % вычисление координат узлов сетки >> y=feval(f,x); % вычисление значений функции в узлах сетки % вычисление интеграла методом трапеций >> s=0; for i=2:N-1 s=s+y(i); End; Ft=(0.5*y(1)+s+0.5*y(N))*dx Ft = 1.0000 >> Ft-1 ans = -5.1456e-008
38. Аналитически найти теоретическую погрешность при численном вычислении интеграла Для нахождения зависимостей погрешности вычисления определенного интеграла на отрезке
Тогда интеграл от данной функции на отрезке
Погрешность формулы трапеций . Так как значение интеграла на отрезке
Заменив в (6.25) первый член выражением (6.23), значение функции в точке
раскрыв скобки и приведя подобные, обнаруживаем, что член, пропорциональный первой производной функции, сокращается, и погрешность на одном отрезке равна
39. Вычислить значение интеграла Пример 6.2. Вычисление интеграла >> f=inline('sin(x)'); % задание подынтегральной функции >> Xmin=0; >> Xmax=pi/2; >> N=2001; >> i=1:N; >> dx=(Xmax-Xmin)/(N-1); % шаг интегрирования >> x=Xmin:dx:Xmax; % вычисление координат узлов сетки >> y=feval(f,x); % вычисление значений функции в узлах сетки % вычисление интеграла методом Симпсона >> s=0; for i=2:N-1 if i-2*ceil(i/2)==0 k=4; Else k=2; End; s=s+k*y(i); End; Fs=(y(1)+s+y(N))*dx/3 Fs = 1.0000 >> Fs-1 ans = E-015
40. Аналитически найти теоретическую погрешность при численном вычислении интеграла Для нахождения зависимостей погрешности вычисления определенного интеграла на отрезке
Тогда интеграл от данной функции на отрезке
Так как формула Симпсона основывается на приближении функции
|


 ,
, 
 задана таблично в узлах
задана таблично в узлах 
 . Выполнить ступенчатую интерполяцию данной функции средствами MATLAB с построением графика.
. Выполнить ступенчатую интерполяцию данной функции средствами MATLAB с построением графика.
 при заданных значениях a, b и
при заданных значениях a, b и 

 с использованием встроенной функции пакета MATLAB.
с использованием встроенной функции пакета MATLAB. с
с методом прямоугольников в пакете MATLAB:
методом прямоугольников в пакете MATLAB: от числа отрезков разбиения интервала интегрирования разложим подынтегральную функцию в ряд Тейлора:
от числа отрезков разбиения интервала интегрирования разложим подынтегральную функцию в ряд Тейлора: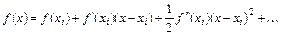 . (6.22)
. (6.22)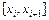 будет равен
будет равен . (6.23)
. (6.23) на отрезке
на отрезке 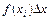 :
: . (6.24)
. (6.24) или, в символической записи,
или, в символической записи,  . Поскольку полное число отрезков равно
. Поскольку полное число отрезков равно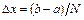 , то полная погрешность метода левых прямоугольников по порядку величины равна
, то полная погрешность метода левых прямоугольников по порядку величины равна  . Аналогично можно показать, что погрешность метода правых прямоугольников также пропорциональна
. Аналогично можно показать, что погрешность метода правых прямоугольников также пропорциональна  .
. , полученное методом средних прямоугольников
, полученное методом средних прямоугольников  (4.24), откуда
(4.24), откуда 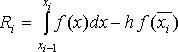 (4.25)
(4.25) разложим подынтегральную функцию
разложим подынтегральную функцию  в ряд Тейлора около средней точки
в ряд Тейлора около средней точки 
 (4.26)
(4.26)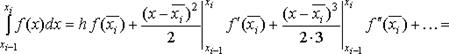
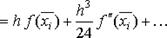 (4.27)
(4.27) , обращаются в нуль. Подставляя полученное соотношение в формулу (4.25), получим
, обращаются в нуль. Подставляя полученное соотношение в формулу (4.25), получим  При малой величине шага интегрирования h основной вклад в погрешность
При малой величине шага интегрирования h основной вклад в погрешность  вычисления интеграла на отрезке
вычисления интеграла на отрезке 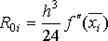 (4.28)
(4.28) определиться путем суммирования погрешностей на каждом отрезке
определиться путем суммирования погрешностей на каждом отрезке  (4.29)
(4.29)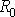 , называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок точности.
, называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок точности.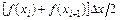 , то погрешность равна
, то погрешность равна (6.25)
(6.25) - разложением в ряд Тэйлора:
- разложением в ряд Тэйлора: ,
, »
»  »
»  . Следовательно, полная погрешность формулы трапеций на отрезке
. Следовательно, полная погрешность формулы трапеций на отрезке 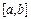 по порядку величины равна
по порядку величины равна  .
.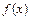 параболой, можно ожидать, что в данном случае погрешность по порядку величины будет определяться членами, пропорциональными третьей производной функции. Однако последовательное повторение действий, выполненных при оценке погрешности метода трапеций, показывает, что эти члены сокращаются в силу их симметричности, поэтому в разложении в ряд Тейлора следует удержать член, пропорциональный
параболой, можно ожидать, что в данном случае погрешность по порядку величины будет определяться членами, пропорциональными третьей производной функции. Однако последовательное повторение действий, выполненных при оценке погрешности метода трапеций, показывает, что эти члены сокращаются в силу их симметричности, поэтому в разложении в ряд Тейлора следует удержать член, пропорциональный  . Следовательно, погрешность формулы Симпсона на отрезке
. Следовательно, погрешность формулы Симпсона на отрезке  , а полная погрешность на отрезке
, а полная погрешность на отрезке  .
.


