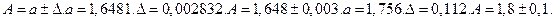Абсолютная и относительная погрешность числа.
по курсу «Информатика»
Выполнил: Финошкин К.И. Проверил: Савченко О.Г. Дата:
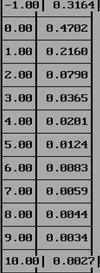
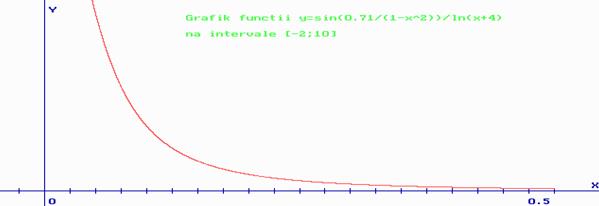
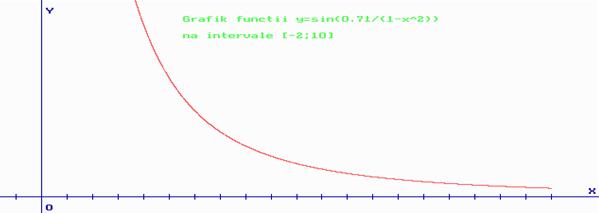
Самара 2014 Построение графика функции. program nnn; uses graph,crt; function F1(x:real):real; begin F1:=cos(0.71/(1+x*x))/ln(x+4); end; function F2(x:real):real; begin F2:=sin(0.71/(1+x*x))/ln(x+4); end; function F3(x:real):real; begin F3:=sin(0.71/(1+x*x)); end; var xn, xk,mx,my,dx,y:real; max,x:real; x0,y0,i,n,c,o:integer; s:string; begin clrscr; writeln('1 - cos(0.71/(1+x*x))/ln(x+4)'); writeln('2 - sin(0.71/(1+x*x))/ln(x+4)'); writeln('3 - sin(0.71/(1+x*x))'); writeln('0 - exit'); readln(o); case o of 1: begin clrscr; xn:=-2;xk:=10; {интервал по Х}max:=abs(F1(xn)); dx:=1; x:=xn; writeln('┌────┬───────┐'); writeln('│ x │ y │'); n:=round((xk-xn)/dx)+1; for i:=1 to n do begin y:=F1(x); writeln('├────┼───────┤'); writeln('│',x:4:2,'│',y:7:4,'│'); x:=x+dx; end; writeln('└────┴───────┘'); readln; while x<=xk do begin if abs(F1(x))>max then max:=abs(F1(x)); x:=x+0.01; end; writeln('max y= ',max:5:2); writeln('min y= ',F1(xk):5:2); readln; initgraph(x0,x0,'c:\tp\bgi\egavga.bgi'); x0:=50; mx:=(getmaxX-2*x0)/xk; {масштаб по Х}y0:=getmaxY div 2; my:=(y0-30)/max; line(0,y0,getmaxX,y0); {оси}line(x0,0,X0,getmaxY); for i:=1 to 2*trunc(xk) do {максимальное количество засечек в одну сторону}begin line(x0-3,y0-round(i*my/2),x0+3,y0-round(i*my/2)); {засечки на оси У}line(x0-3,y0+round(i*my/2),x0+3,y0+round(i*my/2)); str(i/2:0:1,s); {подпись оси У} outtextXY(x0-25,y0-round(i*my/2),s); {соответственно засечкам}outtextXY(x0-30,y0+round(i*my/2),'-'+s); line(x0+round(i*mx/2),y0-3,x0+round(i*mx/2),y0+3); {засечки на оси Х}line(x0-round(i*mx/2),y0-3,x0-round(i*mx/2),y0+3); {подпись оси Х}outtextXY(x0-round(i*my/2),y0+10,s); outtextXY(x0+round(i*my/2),y0+10,+s); end; {центр}outtextXY(x0+5,y0+10,'0'); {подписи концов осей}outtextXY(getmaxX-10,y0-10,'X'); outtextXY(x0+5,10, 'Y'); {график}x:=xn; dx:=0.001; while x<=xk do begin putpixel(x0+round(x*mx),y0-round(F1(x)*my),12); x:=x+dx; end; {название}setcolor(10); outtextXY(200,20,'Grafik functii y=cos(0.71/(1-x^2))/ln(x+4)'); outtextXY(200,40,'na intervale [-2;10]'); readln; end; 2: begin clrscr; xn:=-2;xk:=10; max:=abs(F2(xn)); dx:=1; x:=xn; writeln('┌────┬───────┐'); writeln('│ x │ y │'); n:=round((xk-xn)/dx)+1; for i:=1 to n do begin y:=F2(x); writeln('├────┼───────┤'); writeln('│',x:4:2,'│',y:7:4,'│'); x:=x+dx; end; writeln('└────┴───────┘'); readln; while x<=xk do begin if abs(F2(x))>max then max:=abs(F2(x)); x:=x+0.01; end; writeln('max y= ',max:5:2); writeln('min y= ',F2(xk):5:2); readln; initgraph(x0,x0,'c:\tp\bgi\egavga.bgi'); x0:=50; mx:=(getmaxX-2*x0)/xk; y0:=getmaxY div 2; my:=(y0-30)/max; line(0,y0,getmaxX,y0); line(x0,0,X0,getmaxY); for i:=1 to 2*trunc(xk) do begin line(x0-3,y0-round(i*my/2),x0+3,y0-round(i*my/2)); line(x0-3,y0+round(i*my/2),x0+3,y0+round(i*my/2)); str(i/2:0:1,s); outtextXY(x0-25,y0-round(i*my/2),s); outtextXY(x0-30,y0+round(i*my/2),'-'+s); line(x0+round(i*mx/2),y0-3,x0+round(i*mx/2),y0+3); line(x0-round(i*mx/2),y0-3,x0-round(i*mx/2),y0+3); outtextXY(x0-round(i*my/2),y0+10,s); outtextXY(x0+round(i*my/2),y0+10,+s); end; outtextXY(x0+5,y0+10,'0'); outtextXY(getmaxX-10,y0-10,'X'); outtextXY(x0+5,10, 'Y'); x:=xn; dx:=0.001; while x<=xk do begin putpixel(x0+round(x*mx),y0-round(F2(x)*my),12); x:=x+dx; end; setcolor(10); outtextXY(200,20,'Grafik functii y=sin(0.71/(1-x^2))/ln(x+4)'); outtextXY(200,40,'na intervale [-2;10]'); readln; end; 3: begin clrscr; xn:=-2;xk:=10; max:=abs(F3(xn)); dx:=1; x:=xn; writeln('┌────┬───────┐'); writeln('│ x │ y │'); n:=round((xk-xn)/dx)+1; for i:=1 to n do begin y:=F3(x); writeln('├────┼───────┤'); writeln('│',x:4:2,'│',y:7:4,'│'); x:=x+dx; end; writeln('└────┴───────┘'); readln; while x<=xk do begin if abs(F3(x))>max then max:=abs(F3(x)); x:=x+0.01; end; writeln('max y= ',max:5:2); writeln('min y= ',F3(xk):5:2); readln; initgraph(x0,x0,'c:\tp\bgi\egavga.bgi'); x0:=50; mx:=(getmaxX-2*x0)/xk; y0:=getmaxY div 2; my:=(y0-30)/max; line(0,y0,getmaxX,y0); line(x0,0,X0,getmaxY); for i:=1 to 2*trunc(xk) do begin line(x0-3,y0-round(i*my/2),x0+3,y0-round(i*my/2)); line(x0-3,y0+round(i*my/2),x0+3,y0+round(i*my/2)); str(i/2:0:1,s); outtextXY(x0-25,y0-round(i*my/2),s); outtextXY(x0-30,y0+round(i*my/2),'-'+s); line(x0+round(i*mx/2),y0-3,x0+round(i*mx/2),y0+3); line(x0-round(i*mx/2),y0-3,x0-round(i*mx/2),y0+3); outtextXY(x0-round(i*my/2),y0+10,s); outtextXY(x0+round(i*my/2),y0+10,+s); end; outtextXY(x0+5,y0+10,'0'); outtextXY(getmaxX-10,y0-10,'X'); outtextXY(x0+5,10, 'Y'); x:=xn; dx:=0.001; while x<=xk do begin putpixel(x0+round(x*mx),y0-round(F3(x)*my),12); x:=x+dx; end; setcolor(10); outtextXY(200,20,'Grafik functii y=sin(0.71/(1-x^2))'); outtextXY(200,40,'na intervale [-2;10]'); readln; end; 0: exit; else begin writeln('ne verno, nazhmite Enter i poprobuyte snova'); readln; end; end; end.
Результат (по порядку):
Абсолютная и относительная погрешность числа. Дано приближенное число и относительная погрешность числа. Записать число с явным указанием погрешности. Приближенным числом а называется число, незначительно отличающееся от точного числа А и заменяющее его в вычислениях. Определение. Под абсолютной погрешностью Δ приближенного числа
|

 Блок-схема:
Блок-схема:

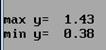



 понимается разность
понимается разность 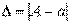 Отсюда следует, что
Отсюда следует, что 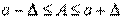 или
или 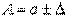 . Относительной погрешностью б приближенного числа а называется отношение абсолютной погрешности Δ этого числа к модулю точного числа.
. Относительной погрешностью б приближенного числа а называется отношение абсолютной погрешности Δ этого числа к модулю точного числа.
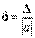 .
.