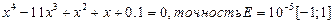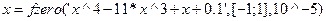Перечислить способы отделения корней. Как реализовать графический способ отделения корней в MATLAB, привести пример М-файла сценария.
f(x)=0(1), x[a,b]. значения x*, которые образуют f(x) в 0 называется корнем уравнения (1). Способы: табличный, графический, современные(используя компьютер), метод половинного деления. Пример графич способа: Абсцисса точки пересечения графиков Файл-сценарий 2.1. % (графический способ отделения корня уравнения (8)) % file_2_1 1; x=0:0.1:1; % массив значений аргумента x 2; y=x.^2; z=exp(-3*x); % вычисление значений функций 3; plot(x,y,x,z) % построение графиков 4; grid on % нанесение координатной сетки Пересечение графиков даст ответ. 15. Метод дихотомии (половинного деления): Его ещё называют методом дихотомии. Этот метод решения уравнений отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [ a, b ]. Метод половинного деления сходится для любых непрерывных функций f (x) в том числе недифференцируемых. Разделим отрезок [ a, b ] пополам точкой с=(а+в)/2. Если f(c)
Пример. Решить в пакете MATLAB уравнение с заданной точностью на заданном отрезке с использованием функции fzero. %построим график. e=f(x) %проверка
|
. 
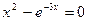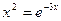
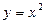
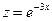
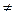0(что практически наиболее вероятно), то возможны два случая: либо f (x) меняет знак на отрезке [ a, c ] (Рис. 3.8), либо на отрезке [ c, b ].
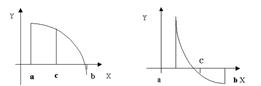Недостатки: метод медленный, не работает с системами.
