В случае ступенчатого регулирования скорости изменение частот вращения подчиняется закону геометрического ряда, в котором каждая последующая частота отличается от предыдущей в 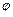 раз (где
раз (где 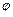 - знаменатель ряда). Целесообразность применения геометрического ряда при проектировании коробок передач впервые была доказана в 1876 году академиком А.В. Гадолиным. Геометрический ряд позволяет:
- знаменатель ряда). Целесообразность применения геометрического ряда при проектировании коробок передач впервые была доказана в 1876 году академиком А.В. Гадолиным. Геометрический ряд позволяет:
- создавать сложные коробки передач из элементарных двухваловых механизмов;
- обеспечить постоянную относительную потерю скорости для всех интервалов частот вращения, т.е. дает экономические преимущества по сравнению с другими рядами.
Относительная потеря скорости 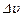 резания может быть представлена следующим образом
резания может быть представлена следующим образом
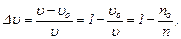
где 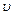 и
и  - соответственно требуемая и действительная скорости резания, м/мин;
- соответственно требуемая и действительная скорости резания, м/мин; 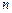 и
и  - соответственно требуемая и действительная частоты вращения шпинделя, об/мин.
- соответственно требуемая и действительная частоты вращения шпинделя, об/мин.
Из приведенной зависимости следует, что относительная потеря 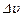 будет тем меньше, чем меньше интервалы между соседними частотами вращения, чем ближе, следовательно, будут
будет тем меньше, чем меньше интервалы между соседними частотами вращения, чем ближе, следовательно, будут  и
и 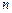 .
.
Если станок имеет ряд частот вращения шпинделя 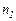 ,
, 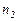 ,
, 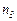 , …,
, …,  , соответствующих геометрическому ряду, то обозначив
, соответствующих геометрическому ряду, то обозначив 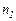 =
=  ;
; 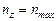 ;
;  - число частот вращения и разложив члены ряда по возрастающей степени, можно записать
- число частот вращения и разложив члены ряда по возрастающей степени, можно записать
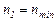 ;
; 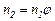 ;
; 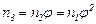 ; …;
; …;  , откуда
, откуда 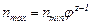 .
.
Знаменатель геометрического ряда
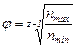 ,
,
где  и
и 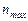 - наименьшая и наибольшая частоты вращения шпинделя.
- наименьшая и наибольшая частоты вращения шпинделя.
Выразим относительную потерю скорости 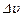 через знаме-
через знаме-
натель ряда 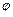
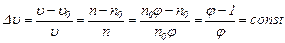 .
.
Так как значение 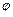 для данного ряда – величина постоянная, то относительная потеря скорости является величиной
для данного ряда – величина постоянная, то относительная потеря скорости является величиной
постоянной, зависящей только от знаменателя геометрического ряда.
При проектировании коробок передач стандартные значения знаменателя геометрического ряда 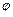 составляют: 1,06; 1,12; 1,26; 1,41; 1,58, 1,78, 2.
составляют: 1,06; 1,12; 1,26; 1,41; 1,58, 1,78, 2.

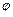 раз (где
раз (где 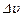 резания может быть представлена следующим образом
резания может быть представлена следующим образом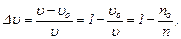
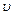 и
и  - соответственно требуемая и действительная скорости резания, м/мин;
- соответственно требуемая и действительная скорости резания, м/мин; 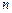 и
и  - соответственно требуемая и действительная частоты вращения шпинделя, об/мин.
- соответственно требуемая и действительная частоты вращения шпинделя, об/мин.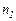 ,
, 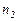 ,
, 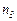 , …,
, …,  , соответствующих геометрическому ряду, то обозначив
, соответствующих геометрическому ряду, то обозначив  ;
; 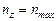 ;
;  - число частот вращения и разложив члены ряда по возрастающей степени, можно записать
- число частот вращения и разложив члены ряда по возрастающей степени, можно записать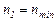 ;
; 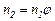 ;
; 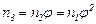 ; …;
; …;  , откуда
, откуда 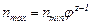 .
.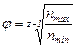 ,
,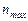 - наименьшая и наибольшая частоты вращения шпинделя.
- наименьшая и наибольшая частоты вращения шпинделя.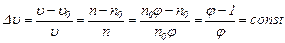 .
.


