Проектирование технически обоснованных
производственных норм 2.1. Исходные данные Исходными данными являются результаты наблюдений в виде замеров времени оперативной работы по отдельным операциям рабочего процесса.
Определим нормативную трудоемкость каждой отдельной рабочей операции, устанавливаемой на измеритель первичной продукции. За нормативную трудоемкость принимается средняя арифметическая величина значений ряда размеров затрат труда, признанных равновероятными. Чтобы определить, все ли значения ряда равновероятны, следует: 1) упорядочить ряд затрат труда (расположить значения ряда в возрастающей последовательности); 2) определить коэффициент разбросанности значений ряда.
1. Строповка 0,5 1 1 1 5 0,63 0,77 0,5 0,52 0,81 мин 0,5 0,5 0,52 0,63 0,77 0,81 1 1 1 5 мин n=10
Кр > 2, проверка хронометражного ряда выполняется по методу нахождения средней квадратичной ошибки, в соответствии с ним улучшению подлежит такой ряд, в котором относительная величина средней квадратичной ошибки превышает установленное значение для данного ряда, т. е. Еотн > [Еотн], то тогда ряд подлежит улучшению.
Вероятное значение средней квадратичной ошибки
К1 ≥ Кn, исключить следует наибольшее значение - 5 Новый ряд: 0,5 0,5 0,52 0,63 0,77 0,81 1 1 1 мин n=9
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
где Σаi – сумма всех значений проверяемого ряда; n – число значений в ряду; an – наибольшее значение ряда; а1 – наименьшее значение ряда; К – коэффициент, учитывающий количество наблюдений.
Все значения ряда равновероятны.
2. Подъем, подача. 1,5 1,6 1,5 1,5 2 2 2,5 мин 1,5 1,5 1,5 1,6 2 2 2,5 мин n=7, k=1,1
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
amax < an, исключить следует наибольшее значение в ряду – 2,5 Новый ряд: 1,5 1,5 1,5 1,6 2 2 мин n=6, k=1,2
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда.
Все значения ряда равновероятны.
3. Устройство постели 2 1,52 2 1,03 2 0,19 2 2 мин 0,19 1,03 1,52 2 2 2 2 2 мин n=8
Кр > 2, проверка хронометражного ряда выполняется по методу нахождения относительной средней квадратичной ошибки. В соответствии с ним улучшению подлежит такой ряд, в котором относительная величина средней квадратичной ошибки (Еотн) превышает установленное допустимое ее значение для данного ряда, т.е. если Еотн > [Еотн] Вероятное значение средней квадратичной ошибки
К1 < Кn исключить следует наименьшее значение в ряду – 0,19 Новый ряд: 1,03 1,52 2 2 2 2 2 мин n=7, k=1,1
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
amin > а1, исключить следует наименьшее значение в ряду – 1,03 Новый ряд: 1,52 2 2 2 2 2 мин n=6, k=1,2
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
amin > а1, исключить следует наименьшее значение в ряду – 1,52 Новый ряд: 2 2 2 2 2 мин n=5
Кр≤1,3 можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда
4. Установка 4 3 4 4 5 8 4 4 4 мин 3 4 4 4 4 4 4 5 8 мин n=9
Кр > 2, проверка хронометражного ряда выполняется по методу нахождения относительной средней квадратичной ошибки. В соответствии с ним улучшению подлежит такой ряд, в котором относительная величина средней квадратичной ошибки (Еотн) превышает установленное допустимое ее значение для данного ряда, т.е. если Еотн > [Еотн] Вероятное значение средней квадратичной ошибки
К1 ≥ Кn, исключить следует наибольшее значение – 8 Новый ряд: 3 4 4 4 4 4 4 5 мин n=8, k=1,1
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
amax < an, amin > а1, исключить следует наибольшее и наименьшее значения в ряду – 5 и 3 Новый ряд: 4 4 4 4 4 4 мин n=6
Кр≤1,3 можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда
5. Выверка 5 4 5 5 5 3 8 5 мин 3 4 5 5 5 5 5 8 мин n=8
Кр > 2, проверка хронометражного ряда выполняется по методу нахождения относительной средней квадратичной ошибки. В соответствии с ним улучшению подлежит такой ряд, в котором относительная величина средней квадратичной ошибки (Еотн) превышает установленное допустимое ее значение для данного ряда, т.е. если Еотн > [Еотн] Вероятное значение средней квадратичной ошибки
К1 ≥ Кn, исключить следует наибольшее значение – 8 Новый ряд: 3 4 5 5 5 5 5 мин n=7, k=1,1
1,3 < Кр ≤ 2, проверка хронометражного ряда производится по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда (а1 и аn) с предельно допустимыми значениями и решение вопроса о сокращении проверенных значений в ряду. Необходимо определить amin и amax
amin > а1, исключить следует наибольшее и наименьшее значения в ряду –3 Новый ряд: 4 5 5 5 5 5 мин n=6
Кр≤1,3 можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда
6. Расстраповка 1 1 1 1 мин 1 1 1 1 мин
Кр≤1,3 можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда
7. Очистка места установки 1,9 мин
8. Разметка места установки 2,0 мин
9. Зацепка ящика с раствором 0,60 мин
10. Прием ящика с раствором 0,60 мин
11. Зацепка порожнего ящика 0,60 мин
12. Отцепка порожнего ящика 0,60 мин
|

 =
=  =10
=10

 =
= 




 =2
=2 ,
,
 =
= 
 =
=  =1,67
=1,67 =
=  < an
< an =
=  < a1
< a1 =1,33
=1,33 > an
> an < a1
< a1







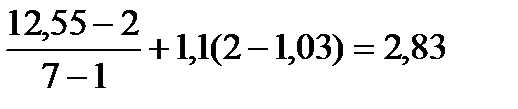 >an
>an > a1
> a1
 >an
>an > a1
> a1




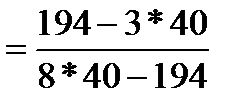



 <an
<an > a1
> a1








 >an
>an > a1
> a1






