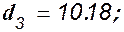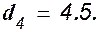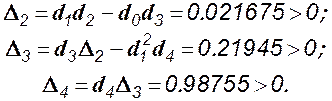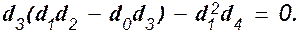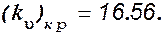АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ УПРАВЛЕНИЯ
Лабораторная работа № 2
АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ УПРАВЛЕНИЯ
Цель работы: · Изучить методику оценки устойчивости системы управления и вычисления запасов устойчивости. Содержание работы: · Определение передаточной функции разомкнутой системы; · Определение передаточной функции замкнутой системы; · Исследование системы на устойчивость по критериям Гурвица и Михайлова. Работа с использованием пакета SIAM: · Определение запасов устойчивости по ЛЧХ для заданного k; · Построение АФЧХ системы, оценка устойчивости и запасов устойчивости по критерию Найквиста для заданного k; · Построение переходной функции h(t) для трех значений коэффициента усиления системы: k < kкр, k = kкр, k > kкр. Критический коэффициент усиления kкр определяется экспериментальным путем.
Исходные данные: · Значения коэффициентов k и kw из таблицы 2.1;
Т = 0,08с для всех вариантов; ·
Значения коэффициентов k2,ξ и постоянных времени Т1 и Т2 задаются в соответствии с вариантом из таблицы 2.2. Порядок выполнения работы на ПК (пакет SIAM - siam-s.exe).
ü Ввести формулы: M0=B*C M1=1+M0*E M2=M0/M1 M3=M2*A M4=M3*D L=M4 ü После нажатия на “ENTER” строится ЛЧХ; ü F3 – большой график; ü F4 – АФЧХ; ü “Esc”- выход в главное меню. ü F7 – моделирование переходного процесса; ü F2 – выбор метода (задать tk = 5…10c); ü F3 – счет; ü F6 – график (подвести курсор к выходному блоку и нажать “ENTER”); ü F4 – режим редактирования блоков (изменение k).
Для передаточной функции разомкнутой системы можно записать
где
Передаточная функция замкнутой системы примет вид
где Составим определитель Гурвица
Оценим устойчивость системы для следующих значений параметров:
При этих значениях для коэффициентов характеристического уравнения получим
Следовательно, все коэффициенты характеристического уравнения замкнутой системы положительны и
Условия устойчивости выполнены и система при избранных параметрах устойчива. Определим критическое значение передаточного числа по углу тангажа, для чего приравняем третий диагональный определитель нулю и сделаем преобразования.
Отсюда
В последнем выражении только d3 и d4 являются функциями коэффициента ku и подставив их в него, получим квадратное уравнение относительно этого коэффициента
Решив это уравнение, получим критическое значение передаточного числа по углу тангажа
Система устойчива, если ku<16.56.
|



 _ _
_ _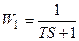
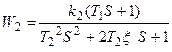
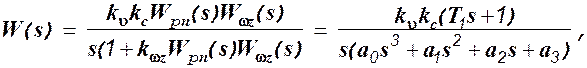
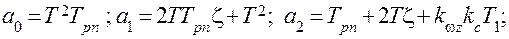



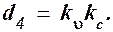
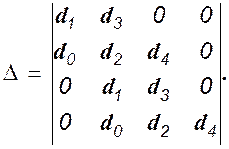

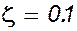 .
.