Само название говорит о том, что граница, разделяющая в признаковом пространстве области различных образов, описывается линейной функцией (рис. 4)
 =
=  .
.
Рис. 4. Линейное решающее правило для распознавания
двух образов
Одна граница при этом разделяет области двух образов. Если  >2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать
>2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать  =2. Если на множестве объектов выполняется условие
=2. Если на множестве объектов выполняется условие


 ,
,
если  – реализация первого образа
– реализация первого образа 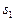 ,
,
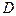

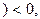
если  – реализация второго образа
– реализация второго образа  ,
,
то образы 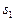 и
и  называют линейно разделимыми.
называют линейно разделимыми.
Существуют различные методы построения линейных решающих правил. Рассмотрим один из них, реализованный в 50-х годах Розенблатом, в устройствах распознавания изображений, названных персептронами (рис. 5).
Пусть
где 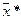 – некоторый объект одного из образов,
– некоторый объект одного из образов, 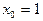 .
.

Рис. 5. Упрощённая схема однослойного персептрона
Выбор  осуществляется пошаговым образом.
осуществляется пошаговым образом.  Текущее значение
Текущее значение  заменяется новым
заменяется новым 
 после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу:
после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу:
1.  , если
, если  и
и  или если
или если  и
и 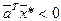 .
.
2.  , если
, если  и
и  ,
,  .
.
3.  , если
, если  и
и  .
.
Это правило вполне логично. Если очередной объект системой классифицирован правильно, то нет оснований изменять  . В случае (2)
. В случае (2)  следует изменить так, чтобы увеличить
следует изменить так, чтобы увеличить  . Предложенное правило удовлетворяет этому требованию. Действительно,
. Предложенное правило удовлетворяет этому требованию. Действительно,
 .
.
Соответственно в случае (3)  .
.
Важное значение имеет выбор  . Можно, в частности, выбрать
. Можно, в частности, выбрать  . При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения
. При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения  , при которых
, при которых

 , если
, если  ,
,

 , если
, если  .
.
Если же выборки линейно неразделимы (рис. 6), то сходимость отсутствует и оценку  , минимизирующую число неправильных распознаваний, находят методом стохастической аппроксимации.
, минимизирующую число неправильных распознаваний, находят методом стохастической аппроксимации.

 =
=  .
.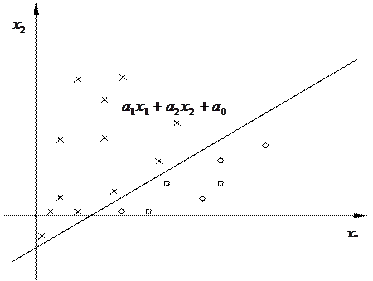
 >2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать
>2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать 

 ,
, – реализация первого образа
– реализация первого образа 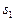 ,
,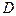

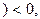
 ,
,

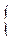
 если
если 

 , если
, если 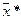 – некоторый объект одного из образов,
– некоторый объект одного из образов, 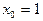 .
.
 осуществляется пошаговым образом.
осуществляется пошаговым образом.  Текущее значение
Текущее значение  после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу:
после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу: , если
, если  и
и  или если
или если  и
и 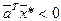 .
. , если
, если  ,
,  .
. , если
, если  .
. . Предложенное правило удовлетворяет этому требованию. Действительно,
. Предложенное правило удовлетворяет этому требованию. Действительно, .
. .
. . Можно, в частности, выбрать
. Можно, в частности, выбрать  . При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения
. При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения 
 , если
, если 


