Метод потенциальных функций
Название метода в определённой степени связано со следующей аналогией (для простоты будем считать, что распознаётся два образа). Представим себе, что объекты являются точками
Рис. 8. Иллюстрация синтеза потенциальной функции
Функцию, описывающую распределение электростатического потенциала в таком поле, можно использовать в качестве решающего правила (или для его построения). Если потенциал точки
Распознавание может осуществляться следующим способом. В точке При большом объёме обучающей выборки эти вычисления достаточно громоздки, и зачастую выгоднее вычислять не Выбор вида потенциальных функций – дело непростое. Например, если они очень быстро убывают с ростом расстояния, то можно добиться безошибочного разделения обучающих выборок. Однако при этом возникают определённые неприятности при распознавании неопознанных объектов (снижается достоверность принимаемого решения, возрастает зона неопределённости). При слишком "пологих" потенциальных функциях может необоснованно увеличиться количество ошибок распознавания, в том числе и на обучающих объектах. Определённые рекомендации в этом отношении можно получить, рассматривая метод потенциальных функций со статистических позиций (восстановление плотности распределения вероятностей
|

 некоторого пространства
некоторого пространства  . В эти точки будем помещать заряды
. В эти точки будем помещать заряды  , если объект принадлежит образу
, если объект принадлежит образу 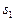 , и
, и  , если объект принадлежит образу
, если объект принадлежит образу  (рис. 8).
(рис. 8).
 – потенциальная функция, порождаемая одиночным объектом;
– потенциальная функция, порождаемая одиночным объектом; – суммарная потенциальная функция, порождённая обучающей последовательностью
– суммарная потенциальная функция, порождённая обучающей последовательностью , создаваемый единичным зарядом, находящимся в
, создаваемый единичным зарядом, находящимся в  , то общий потенциал в
, то общий потенциал в  зарядами, равен
зарядами, равен
 и монотонно убывающая до нуля при
и монотонно убывающая до нуля при 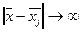 .
. . Если он оказывается положительным, то объект относят к образу
. Если он оказывается положительным, то объект относят к образу  или разделяющей границы по выборке с использованием процедуры типа стохастической аппроксимации). Этот вопрос выходит за рамки данного курса лекций.
или разделяющей границы по выборке с использованием процедуры типа стохастической аппроксимации). Этот вопрос выходит за рамки данного курса лекций.


