Обучение в данном случае состоит в запоминании всех объектов обучающей выборки. Если системе предъявлен нераспознанный объект 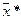 , то она относит этот объект к тому образу (рис. 7), чей "представитель" оказался ближе всех к
, то она относит этот объект к тому образу (рис. 7), чей "представитель" оказался ближе всех к 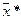 .
.

Рис. 6. Пример линейно неразделимых множеств
Рис. 7. Решающее правило "Минимум расстояния
до ближайшего соседа"
Это правило ближайшего соседа. Правило  ближайших соседей состоит в том, что строится гиперсфера объёма
ближайших соседей состоит в том, что строится гиперсфера объёма  с центром в
с центром в 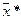 . Распознавание осуществляется по большинству "представителей" какого-либо образа, оказавшихся внутри гиперсферы. Здесь тонкость состоит в том, чтобы правильно (разумно) выбрать объём гиперсферы.
. Распознавание осуществляется по большинству "представителей" какого-либо образа, оказавшихся внутри гиперсферы. Здесь тонкость состоит в том, чтобы правильно (разумно) выбрать объём гиперсферы.  должен быть достаточно большим, чтобы в гиперсферу попало относительно большое число "представителей" разных образов, и достаточно маленьким, чтобы не сгладить нюансы разделяющей образы границы. Метод ближайших соседей имеет тот недостаток, что требует хранения всей обучающей выборки, а не её обобщённого описания. Зато он даёт хорошие результаты на контрольных испытаниях, особенно при больших количествах объектов, предъявленных для обучения.
должен быть достаточно большим, чтобы в гиперсферу попало относительно большое число "представителей" разных образов, и достаточно маленьким, чтобы не сгладить нюансы разделяющей образы границы. Метод ближайших соседей имеет тот недостаток, что требует хранения всей обучающей выборки, а не её обобщённого описания. Зато он даёт хорошие результаты на контрольных испытаниях, особенно при больших количествах объектов, предъявленных для обучения.
Для сокращения числа запоминаемых объектов можно применять комбинированные решающие правила, например сочетание метода дробящихся эталонов и ближайших соседей.
В этом случае запоминанию подлежат те объекты, которые попали в зону пересечения гиперсфер какого-либо уровня. Метод ближайших соседей применяется лишь для тех распознаваемых объектов, которые попали в данную зону пересечения. Иными словами, запоминанию подлежат не все объекты обучающей выборки, а только те, которые находятся вблизи разделяющей образы границы.

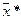 , то она относит этот объект к тому образу (рис. 7), чей "представитель" оказался ближе всех к
, то она относит этот объект к тому образу (рис. 7), чей "представитель" оказался ближе всех к 

 ближайших соседей состоит в том, что строится гиперсфера объёма
ближайших соседей состоит в том, что строится гиперсфера объёма  с центром в
с центром в 


