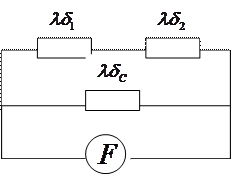
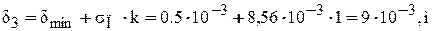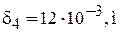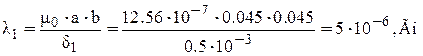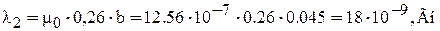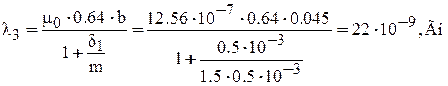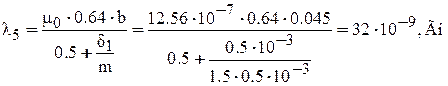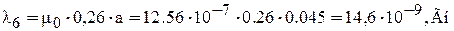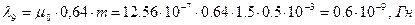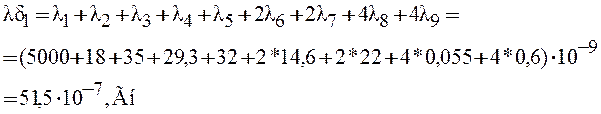Схема замещенияПроводимости рассчитываем методом разбивки поля на простые геометрические фигуры (метод Ротерса).
Принимают обычно m =(1-2)δ.
Рис. 4.4. Схема замещения
Рис.4.3. К расчету магнитной проводимости воздушного зазора методом простых фигур. 4.5.2 Расчет проводимостей производим для пяти зазоров: 1. 2. Выбираем величину зазора значение, которого лежит между первым и третьим зазором. 3. для переменного тока κ=(0,8-1,5), 4. Выбираем величину зазора значение, которого лежит между третьим и пятым зазором. 5. β- провал контакта Фигура 1 - призма высотой δ и основанием а и b
Фигура 2 - Полуцилиндр диаметром δ длиной b
Фигура 3 - половина полого цилиндра
Фигура 4 - четверть цилиндра радиуса δ;
Фигура 5 - четверть полого цилиндра
Фигура 6 – полуцилиндр диаметра δ длиной а
Фигура 7 – половина полого цилиндра длиной а
Фигура 8 – сферический квадрант
Фигура 9 – квадрант сферической оболочки
Полная проводимость воздушного зазора есть сумма всех частичных:
По этой формуле рассчитываем проводимости для всех пяти зазоров.
|
Выделяем простые фигуры согласно рис.4.3. При расчете проводимости данным методом, важное значение имеет выбор параметра m, учитывающего поток с боковых поверхностей полюса магнитной системы. Его значение определяется соотношением величины зазора δ к линейным размерам а и b.
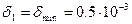м
