Канальное кодирование
Все преимущества цифрового представления сигналов могут быть реализованы только при условии безошибочной передачи данных по каналам связи. Последствия неверно принятого бита данных значительно более серьезны, чем в аналоговом телевидении. Канальное кодирование необходимо для повышения помехоустойчивости передачи данных. Принцип канального кодирования основан на использовании специальных кодов, позволяющих обнаруживать и восстанавливать истинные значения данных, искаженных за счет влияния помех в канале связи. Теоретической основой таких кодов является добавление к передаваемым данным избыточной информации. В простейшем случае ошибки обнаруживают путем добавления к каждому кодовому слову бита, дополняющего число единиц до четного значения. На приемном конце производят проверку на четность. Если кодовая группа не проходит эту проверки, то в ней содержится ошибка. Можно замаскировать эту ошибку, заменяя принятую кодовую комбинацию предыдущей.
Число ошибок, которые корректирующий код может исправить в определенном интервале последовательности двоичных символов, называют исправляющей способностью кода. Основной принцип построения корректирующих кодов состоит в том, что в каждую передаваемую кодовую комбинацию из
Произведение полиномов получают по обычному правилу перемножения степенных функций, однако получаемые коэффициенты при данной степени Х складываются по
Первое уравнение есть результат умножения на 1; второе – на Х. При формировании результата суммируют по модулю 2 коэффициенты при одинаковых степенях Х. Суммирование степеней производят по модулю
Первый многочлен получился после умножения на Х, а второй – на Х 2. При суммировании единичные коэффициенты при степени 4 дали нуль.
Наконец, можно сформулировать теорему о делении полиномов: для каждой пары полиномов С(х) и d(x), d(x) ≠ 0 существует единственная пара полиномов q(x) — частное и r(х) — остаток, такие, что С (х) = q(x)× d(x) + r(х), (1.58) где степень остатка r(х) меньше степени делителя d(x). Иными словами, деление полиномов производится по правилам деления степенных функций, при этом операция вычитания заменяется суммированием по mod2. Например:
Еще раз напомним, что при сложении по mod2 сумма двух единиц (то есть коэффициентов двух элементов полинома с одинаковыми степенями) будет равна нулю, а не привычным в десятичной системе счисления двум. И, кроме этого, операции вычитания и сложения по mod2 совпадают. Еще один пример деления полиномов: Пусть нужно разделить
Основная идея помехозащитного кодирования Рида-Соломона заключается в умножении информационного слова, представленного в виде полинома D, на неприводимый полином G [3], известный обеим сторонам, в результате чего получается кодовое слово C, опять-таки представленное в виде полинома. Декодирование осуществляется в обратном порядке: если при делении кодового слова C на полином G декодер получает остаток, то он может рапортовать наверх об ошибке. Соответственно, если кодовое слово разделилось нацело, его передача завершилась успешно. Если степень полинома G (называемого также порождающим полиномом) превосходит степень кодового слова, по меньшей мере, на две степени, то декодер может не только обнаруживать, но и исправлять одиночные ошибки. Если же превосходство степени порождающего полинома над кодовым словом равно четырем, то восстановлению поддаются и двойные ошибки. Короче говоря, степень полинома
Видно, что все получилось правильно.
Получилась разрешенная кодовая группа, показанная выше седьмой. Первые четыре кодовых группы получились для входных кодов, содержащих одну единицу в одной из позиций. Остальные кодовые группы получились путем суммирования по модулю 2 строк порождающей матрицы в сочетаниях, определенных положениями единиц в исходном информационном коде согласно правилу умножения вектора на матрицу. Получилось, что всего 16 разрешенных информационных кодовых групп, или 2k=4 . Запрещенных кодовых групп 2 n -2 k = 128-16=112. Минимальное расстояние по Хеммингу между разрешенными кодовыми группами равно 3, т. е. числу проверочных бит
Среди большого числа циклических кодов к числу наиболее эффективных и широко используемых относятся коды Бозе-Чоудхурия-Хоквингема (БЧХ-коды).
Код Рида-Соломона обладает способностью исправлять пакетные ошибки, когда ошибочные символы следуют друг за другом. Его используют для внешнего кодирования. Код Рида-Соломона требует добавления двух проверочных символов на одну исправляемую ошибку. На каждый пакет общего транспортного потока длиной 188 байт добавляют 16 проверочных байт. Это позволяет исправить 8 байт, искаженных помехой в ходе передачи. Такой код в литературе называют (204, 188, 8). Корректирующей способности этого кода может не хватить для исправления длинного пакета ошибок (импульсная помеха, царапина на лазерном диске и пр.). Важно преобразовать пакетную ошибку в последовательность одиночных ошибок. Простейшим способом такого преобразования является запись кодированного внешним кодером сигнала в память построчно, а считывание по столбцам. Тогда длинная горизонтальная последовательность ошибок превращается в последовательность одиночных ошибок (рис. 9).. Но значительно лучшие результаты получают при использовании перемешивания информации (скремблирования) (рис. 10). Скремблирование применяют и для шифровки передаваемых данных, так как восстановить правильный порядок следования битов при дескремблировании можно только обладая информацией о правилах перестановки битов.
|


 информационных символов вводят
информационных символов вводят  дополнительных двоичных символов. В результате получается новая кодовая комбинация, содержащая
дополнительных двоичных символов. В результате получается новая кодовая комбинация, содержащая  двоичных символов. Этот код называют
двоичных символов. Этот код называют 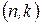 . Избыточность такого кода
. Избыточность такого кода 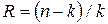 . Из общего числа комбинаций
. Из общего числа комбинаций  разрешенные (правильные)
разрешенные (правильные)  , остальные
, остальные  ошибочные (запрещенные). Появление одной из запрещенных комбинаций на приемной стороне означает, что имеется ошибка. Для оценки корректирующей способности кода используют понятие кодового расстояния Хемминга
ошибочные (запрещенные). Появление одной из запрещенных комбинаций на приемной стороне означает, что имеется ошибка. Для оценки корректирующей способности кода используют понятие кодового расстояния Хемминга  которое определено суммарным числом несовпадающих бит. Одиночная кодовая ошибка дает кодовое расстояние
которое определено суммарным числом несовпадающих бит. Одиночная кодовая ошибка дает кодовое расстояние 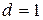 . Следовательно, кодовое расстояние между разрешенными комбинациями должно составлять не менее
. Следовательно, кодовое расстояние между разрешенными комбинациями должно составлять не менее  . Дл обнаружения
. Дл обнаружения  ошибок кодовое расстояние должно быть
ошибок кодовое расстояние должно быть  . Для исправления одиночных ошибок нужно, чтобы кодовое расстояние между двумя любыми разрешенными кодовыми комбинациями было не менее 3. В этом случае принятую запрещенную кодовую комбинацию заменяют ближайшей к ней разрешенной комбинацией. В общем случае для коррекции
. Для исправления одиночных ошибок нужно, чтобы кодовое расстояние между двумя любыми разрешенными кодовыми комбинациями было не менее 3. В этом случае принятую запрещенную кодовую комбинацию заменяют ближайшей к ней разрешенной комбинацией. В общем случае для коррекции 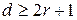 .
. 
 .
.
 . Например:
. Например: . Если при умножении встретится степень большая
. Если при умножении встретится степень большая  на полином
на полином  . Делим в столбик, как обычно! Но нужно помнить, что вычитание эквивалентно сложению, которое ведется по модулю 2!
. Делим в столбик, как обычно! Но нужно помнить, что вычитание эквивалентно сложению, которое ведется по модулю 2!

 Делитель
Делитель
 Результат деления
Результат деления


 -остаток!
-остаток! . Следовательно, кодовое слово должно содержать два дополнительных символа
. Следовательно, кодовое слово должно содержать два дополнительных символа 


 Формирование кодовых групп реализуем путем умножения информационного вектора размером
Формирование кодовых групп реализуем путем умножения информационного вектора размером  , где
, где  , на производящую матрицу размером
, на производящую матрицу размером  , где
, где  . В результате умножения получим векторы кодовых групп размерностью
. В результате умножения получим векторы кодовых групп размерностью  .
. 
 . Значит такой код может обнаруживать две одиночные ошибки и исправлять одну.
. Значит такой код может обнаруживать две одиночные ошибки и исправлять одну.
 ;
; 










