Последовательный стык
Последовательный код организуют из параллельного путем мультиплексирования с тактовой частотой 243 МГц при 8-разрядном кодировании и 270 МГц при 10 разрядном. Каждое 8-битовое слово преобразуют в 9-битовое. Используют инвертированный код без возврата к нулю БВНИ. Этот код изменяет состояние сигнала в середине тактового импульса при передаче единицы; отсутствие изменения означает передачу нуля (рис. 2). Следовательно, передаваемая информация не зависит от полярности сигнала. Скремблирование позволяет выровнять частоту появления нулей и единиц в исходном коде, что необходимо для надежного восстановления тактовых импульсов, которые при последовательной передаче отдельно не передают. Дополнительно скремблирование позволяет защитить передачу от несанкционированного доступа. Тактовые импульсы отдельно не передают, а восстанавливают непосредственно из принятого сигнала (рис. 3). Каждому переходу (из ноля в единицу и наоборот) сопоставляют короткий импульс. Далее эти импульсы расширяют и пропускают через узкополосный фильтр, настроенный на тактовую частоту. Затем, после ограничения, получают прямоугольные тактовые импульсы. Скремблирование осуществляют с использованием псевдослучайной последовательности. Под псевдослучайной последовательностью понимают периодическую последовательность элементов из области значений
Существуют таблицы этих полиномов, например, при скремблировании цифровых ТВ сигналов используют порождающий полином девятой степени Элемент псевдослучайной последовательности
Например, для приведенного выше полинома расчетная формула будет иметь вид:
так как только коэффициенты Важно понимать, что псевдослучайная последовательность регулярная, сформированная по известному закону и может быть воспроизведена, если известен закон (порождающий полином) и начальное слово. Она обладает всеми свойствами собственно случайной последовательности. Например, вероятность нового значения последовательности
Числа нулей и единиц равны. Для генерирования псевдослучайной последовательности организуют регистр сдвига из девяти разрядов с обратными связями из разрядов 9 и 4 (рис. 2). Чтобы начать расчет, нужно задать начальное слово. Это может быть любая комбинация из Скремблирование реализуют на основе формулы суммирования по модулю 2
где На приемной стороне имеется точно такой же генератор псевдослучайной последовательности, что позволяет восстановить исходный видеосигнал
так как Степень порождающего полинома Эффект защиты достигают тем, что для потенциального взломщика неизвестен ни порождающий полином, ни начальное слово псевдослучайной последовательности, которое может быть фрагментом ПСП из, также выбранного по случайному закону.
|

 , где
, где  - основание последовательности. Если
- основание последовательности. Если  , то таких элементов два: ноль и единица. Это регулярная периодическая последовательность, длина (период) которой определена как
, то таких элементов два: ноль и единица. Это регулярная периодическая последовательность, длина (период) которой определена как  , где
, где  - память последовательности. Для формирования ПСП максимальной длины используют неразложимые примитивные полиномы степени
- память последовательности. Для формирования ПСП максимальной длины используют неразложимые примитивные полиномы степени  ноль и единица
ноль и единица
 ,
,
 всегда равен единице.
всегда равен единице. , где коэффициенты
, где коэффициенты  .
. находят путем суммирования по модулю 2 предыдущих значащих элементов, определенных использованным полиномом
находят путем суммирования по модулю 2 предыдущих значащих элементов, определенных использованным полиномом .
. ,
, и
и 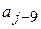 равны единице, а остальные коэффициенты равны нулю.
равны единице, а остальные коэффициенты равны нулю. .
. ,
, - входной сигнал, а
- входной сигнал, а  - выходной.
- выходной.
 ,
, .
. определяет длину псевдослучайной последовательности
определяет длину псевдослучайной последовательности  . Для полинома 9-ой степени псевдослучайная последовательность имеет период 511 элементов. Для усиления эффекта защиты иногда используют порождающий полином 15 степени
. Для полинома 9-ой степени псевдослучайная последовательность имеет период 511 элементов. Для усиления эффекта защиты иногда используют порождающий полином 15 степени  с длиной псевдослучайной последовательности 32767 элементов.
с длиной псевдослучайной последовательности 32767 элементов.


