Арифметичні дії в q-ричній системі числення
Розглянемо основні арифметичні операції: додавання, віднімання. Правила виконання цих операцій в десятковій системі добре відомі. Ці правила можна застосувати і до всіх інших позиційних систем числення. Тільки таблицями додавання і множення треба користуватися особливими для кожної системи. Додавання. Додавання в двійковій системі.
Додавання в вісімковій системі.
При додаванні цифри додаються порозрядно, і якщо при цьому виникає надлишок то він переноситься вліво (формується старший розряд). Приклад. Додамо числа в різних системах числення (СЧ).
Віднімання. Двійкова СЧ. Правила віднімання:
Приклади:
Кодовані позиційні системи числення
Двійково-десяткові коди мають надлишковість, так як для кодування десяткових цифр використовуються тільки 10 комбінацій із 16.
Двійково-десятковий код
В двійково-десятковому (двійково-кодованому) представленні десяткового числа кожна десяткова цифра зображується тетрадою двійкових символів Одержаний таким чином десятковий код, кодований двійковими символами називається Д – кодами. Є деяка множина Д кодів. Це зумовлено наявністю 10 дозволених із 16 можливих комбінацій, які допускає тетрада. Наявність заборонених комбінацій в Д - кодах відрізняє їх від звичайних позиційних систем числення в яких всі комбінації – дозволені. Із всієї множини відомих Д – кодів найбільш поширені в обчислювальній техніці отримали код Д1 прямого заміщення (система 8421) і код Д2 з надлишком 3 (система 8421+3). Із-за заборонених комбінацій, при додаванні чисел в Д – кодах виникає необхідність в корекції результату і трудності в формуванні десяткового переносу в наступну тетраду. Особливості додавання чисел в кожному із Д – кодів різні. Задані числа
де Необхідно отримати
де
Так як найбільше десяткове однорозрядне число 9 то з врахуванням переносу в даний розряд, значення результату розрядного сумування лежить в межах від 0 до 19. При цьому одиниця в другому розряді представляє собою десятковий переніс в наступну тетраду, а суму одержуємо в двійковому коді, який відрізняється від потрібного двійково-десяткового представлення, тобто він потребує корекції. При додаванні чисел в Д кодах можуть виникнути наступні випадки: 1) якщо 2) якщо
де При цьому ознакою неправильного результату є в одному випадку виникнення потетрадного переносу В будь якому із цих випадків необхідно скоректувати результат в даній тетраді введенням поправки +0110, що приведе до виникнення потетрадного переносу і в другому випадку. Корекція обумовлена тим, що кожний переніс забирає із собою із даної тетради 16 одиниць, а приносить в наступну тільки 10 одиниць. Приклад. Додати тетради
Так як
Приклад. Додати тетради
Так як величина Отже, якщо в якщо сума цифр з переносом рівна або більша 10, то відбувається корекція результату тетради введенням поправки +0110, а переніс який при цьому виник додаємо до наступної тетради При цьому, якщо в декількох тетрадах, починаючи з Приклад. Додати два числа:
Приклад:
проводимо корекцію в молодшій тетраді:
проводимо корекцію в другій тетраді:
проводимо корекцію в старшій тетраді:
Контрольні запитання
1. Які системи числення називаються позиційними, непозиційними? 2. Переведіть задані числа із однієї системи числення в іншу. 3. Виконайте арифметичні операції в різних системах числення. 4. Які фактори необхідно враховувати при виборі СЧ.
|












 ,
,  – десяткова цифра
– десяткова цифра  – го розряду;
– го розряду;  – двійкова цифра
– двійкова цифра  ;
; ,
, – двійково-кодовані десяткові цифри (тетради).
– двійково-кодовані десяткові цифри (тетради). при цьому
при цьому  ;
;  ,
, ,
,  - десяткові переноси;
- десяткові переноси; - основа системи числення.
- основа системи числення. , то виконання дій над розрядами тетради по правилах двійкової арифметики зразу отримаємо правильний результат;
, то виконання дій над розрядами тетради по правилах двійкової арифметики зразу отримаємо правильний результат; , то виникає десятковий переніс. Тому сума в даній тетраді повинна бути рівна:
, то виникає десятковий переніс. Тому сума в даній тетраді повинна бути рівна: ,
,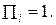
 , в другому поява забороненої комбінації, якщо
, в другому поява забороненої комбінації, якщо  .
. ;
;  при
при  .
. .
. , необхідна корекція результату
, необхідна корекція результату  ,
,
 при
при  .
. належить до заборонених комбінацій, то необхідно ввести поправку виду 0110.
належить до заборонених комбінацій, то необхідно ввести поправку виду 0110. - ї тетради менше 10, то додавання відбувається без поправок;
- ї тетради менше 10, то додавання відбувається без поправок;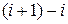 .
. – ї, розрядна сума дорівнює 1001, то переніс приводить до формування забороненої комбінації в
– ї, розрядна сума дорівнює 1001, то переніс приводить до формування забороненої комбінації в  – й тетраді і т.д.
– й тетраді і т.д. і
і  .
. :
:  .
.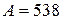 ,
,  .
. ;
; ;
; ;
; .
.


